这是我在QQ群中国数学解题研究会中看到的问题:
若函数$f(x)=m-\sqrt{x+3}$的定义域为$[a,b]$,值域也为$[a,b]$,求实数$m$的取值范围.
正确答案是$\left(-\dfrac 94,-2\right]$.
解 注意到函数$f(x)$为单调递减函数,于是$$\begin{cases} f(a)=b,\\f(b)=a, \end{cases} $$设$A \left( a,f(a)\right) $,$B\left( b,f(b)\right) $,则点$A$、$B$关于直线$y=x$对称.
方法一 以横坐标为参数
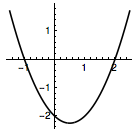
令$s=\sqrt{a+3}$,$t=\sqrt{b+3}$,于是$$\begin{cases} m=s^2-3+t,\\m=t^2-3+s,\end{cases} $$两式相减得$$s+t=1,$$进而可得$$m=s^2-s-2=t^2-t-2,$$因此只需要关于$x$的方程$$m=x^2-x-2$$有两个不等的正实根.
如图,可以得到$m$的取值范围是$\left(-\dfrac 94,-2\right]$.
方法二 以截距为参数
设直线$AB$的方程为$$AB:y=-x+2t,$$该直线与$y=x$相交于点$M(t,t)$,于是要保证$A$、$B$关于直线$y=x$对称,只需要直线$AB$与抛物线$y=m-\sqrt{x+3}$相交且交点横坐标之和为$2t$即可.
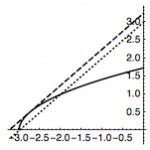
联立整理得$$x^2-(4t-2m+1)x+(2t+m)^2-3=0,$$于是两根之和$$4t-2m+1=2t,$$即$$m=t+\dfrac 12,$$因此问题转化为直线$$AB:y=-x+2t$$与抛物线$$y=t+\dfrac 12-\sqrt{x+3}$$有两个交点,即直线$y=x-t+\dfrac 12$和函数$y=\sqrt{x+3}$的图象有两个交点.
如图,可以得到$-t+\dfrac 12$的取值范围是$\left[3,\dfrac{13}4\right)$,从而$m$的取值范围是$\left(-\dfrac{9}4,-2\right]$.
注 如果注意到抛物线的算术平均性质:
若对称轴为$x$轴方向的抛物线的一条割线与一条切线平行,那么割线与抛物线的两个交点的纵坐标的算术平均数为切线与抛物线的切点的纵坐标.
那么可以优化方法二:
抛物线$f(x)=m-\sqrt{x+3}$的导函数为$$f'(x)=-\dfrac{1}{2\sqrt{x+3}},$$于是斜率为$-1$的切线切点横坐标为$-\dfrac{11}4$,纵坐标为$m-\dfrac 12$,因此可得$$t=m-\dfrac 12.$$
关于抛物线的这条性质的更多应用,可以参考《抛物线的一条有趣性质》,以及《2014年高考山东卷理科压轴题的解答》.