沿着与正方体的体对角线垂直所作截面是高中数学立体几何的学习中经常遇到的问题,例如下面这道试题(来自2014年北京市西城区高三期末理科数学,原题为选择题).
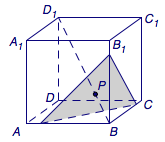
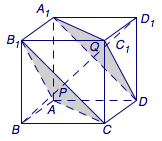
如图,正方体\(ABCD-A_1B_1C_1D_1\)的棱长为\(2\sqrt 3\),动点\(P\)在对角线\(BD_1\)上,过\(P\)作垂直于\(BD_1\)的平面\(\alpha\),记这样得到的截面多边形(含三角形)的周长为\(y\),设\(BP=x\),则当\(x\in [1,5]\)时,函数\(y=f(x)\)的值域为________.
作平面\(\alpha\)与正方体\(ABCD-A'B'C'D'\)的对角线\(AC'\)垂直,使得\(\alpha\)与正方体的每个面都有公共点,记这样得到的截面多边形的面积为\(S\),周长为\(l\),则( )
A.\(S\)和\(l\)均为定值
B.\(S\)为定值,\(l\)不为定值
C.\(S\)不为定值,\(l\)为定值
D.\(S\)和\(l\)均不为定值
那么我们在今天与这些题做个了断:
正方体\(ABCD-A_1B_1C_1D_1\)的棱长为\(1\),动点\(P\)在对角线\(BD_1\)上,过\(P\)作垂直于\(BD_1\)的平面\(\alpha\),记这样得到的截面多边形(含三角形)的周长为\(L\),面积为\(S\),\(BP=x\),作出曲线\(L(x)\)与\(S(x)\).
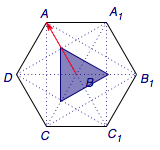
为了看清楚截面,我们作沿着正方体\(ABCD-A_1B_1C_1D_1\)的体对角线\(BD_1\)方向的正投影,并将截面三角形的变化过程绘图如下:
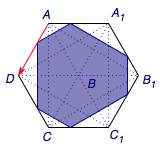
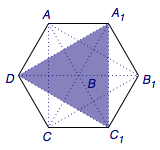
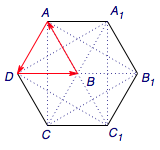
运动的三个阶段可以借助下面两个图帮助想象(\(B\to P\to Q\to D_1\)的三等分线段与\(B\to A\to D\to B\)的等边三角形的分别对应):
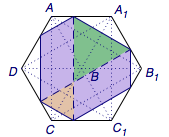
其中第二阶段(六边形阶段)最为复杂,依靠下图可以证明此阶段周长为定值,而面积不为定值(服从二次函数关系).
点评 \(B\to P\to Q\to D_1\)的三等分线段与\(B\to A\to D\to B\)的等边三角形的分别对应是这个解法最为精彩的部分,让人不由得赞叹正方体的美妙!




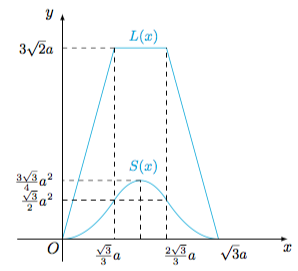
最下面的图中的横坐标有错误。