每日一题[32] 妙用外心解向量题

已知$O$是锐角三角形$ABC$外接圆的圆心，若 $$\frac{\cos B}{\sin C}\overrightarrow{AB}+\frac{\cos C}{\sin B}\overrightarrow{AC}=2m\overrightarrow{AO},$$ 则$m=$________．

等式两边同时对$\overrightarrow{AO}$做数量积，有 $$\frac{\cos B}{\sin C}\overrightarrow{AB}\cdot\overrightarrow{AO}+\frac{\cos C}{\sin B}\overrightarrow{AC}\cdot\overrightarrow{AO}=2m\overrightarrow{AO}\cdot\overrightarrow{AO},$$ 利用数量积的几何意义，有 $$\frac{\cos B}{\sin C}\cdot\frac 12c^2+\frac{\cos C}{\sin B}\cdot\frac 12b^2=2m\cdot R^2,$$ 其中$a,b,c,R$分别表示三角形的三边以及外接圆半径．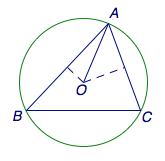

接下来对式子进行变形 $$\frac{\cos B}{\sin C}\cdot\left(\frac c{2R}\right)^2+\frac{\cos C}{\sin B}\cdot\left(\frac b{2R}\right)^2=m,$$

应用正弦定理，并化简，就得到 $$m=\cos B\cdot\sin C+\cos C\cdot\sin B=\sin (B+C)=\sin A.$$

点评    利用数量积处理三角形的外心相关的平面向量问题．

下面给出一道题目作为练习．

已知$O$是三角形$ABC$的外心，$AB=2$，$AC=1$，$\angle BAC=120^\circ$．若 $$\overrightarrow{AO}=m\overrightarrow{AB}+n\overrightarrow{AC},$$ 则$m-n=$________．

答案    $-\dfrac 12$．