用给定基底或者根据具体情形选定基底后对图形中未知向量的分解，是解决向量问题或利用向量解决平面几何问题的重要核心步骤．在对平面向量的分解过程中，平面图形的性质得以代数化，从而可以通过函数、不等式等代数方法进行研究．与此同时，分解的系数也具有鲜明的几何意义，结合这些几何意义往往又可以简化问题．在学习平面向量时，体会这种代数与几何条件的互相对应与转化，对提高数形结合能力大有裨益．下面就通过一道经典的平面向量试题例说这一点．
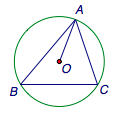
已知\(O\)为\(\triangle ABC\)的外心，\(\cos A=\dfrac{1}{3}\)，若\(\overrightarrow{AO}=\alpha\overrightarrow{AB}+\beta\overrightarrow{AC}\)，则\(\alpha + \beta\)的最大值为________．
记\(A\)、\(B\)、\(C\)所对的边分别为\(a\)、\(b\)、\(c\)，考虑到问题所求与三角形的大小无关，不妨设\(a = 1\)．
如图，此时\(\triangle ABC\)的外接圆固定，即\(B\)、\(C\)、\(O\)为定点，\(A\)在优弧\(BC\)上运动．
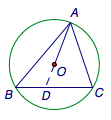
延长\(AO\)交\(BC\)于\(D\)，设\(\overrightarrow{AO}=\lambda\overrightarrow{AD}\)，则\[\overrightarrow{AD}=\dfrac{\alpha}{\lambda}\overrightarrow{AB}+\dfrac{\beta}{\lambda}\overrightarrow{AC}.\]
因为\(D\)在\(BC\)上，因此\(\dfrac{\alpha}{\lambda}+\dfrac{\beta}{\lambda}=1\)，即\(\lambda=\alpha+\beta\)．
于是问题即求\(\lambda\)的最大值，考虑到\[\lambda=\dfrac{{\left|{AO}\right|}}{{\left| {AD}\right|}}=\dfrac{{\left|{AO}\right|}}{{\left|{AO}\right|+\left|{OD}\right|}},\]而\(\left|{AO}\right|\)为定值，因此当\(\left|{OD}\right|\)取最小值，也即\(AD\perp BC\)的时候\(\lambda\)取得最大值．此时
\[\left|{AO}\right|=\dfrac{1}{2}\cdot\dfrac{a}{{\sin A}}=\dfrac{1}{2}\cdot\dfrac{1}{{\dfrac{{\sqrt 8}}{3}}}=\dfrac{{3\sqrt 2}}{8}\qquad\cdots (1)\]
而\(\left|{AB}\right|=\left|{AC}\right|\)，\(\triangle ABC\)为等腰三角形，因此由二倍角公式可得\(\cos\angle BAD=\sqrt{\dfrac{2}{3}}\)．因此
\[\left|{AD}\right|=\dfrac{{\left|{BD}\right|}}{{\tan\angle BAD}}=\dfrac{{\dfrac{1}{2}}}{{\dfrac{1}{{\sqrt 2 }}}}=\dfrac{{\sqrt 2}}{2}\qquad\cdots(2)\]
因此
\[\lambda=\dfrac{{\left|{AO}\right|}}{{\left|{AD}\right|}}=\dfrac{{\dfrac{{3\sqrt 2 }}{8}}}{{\dfrac{{\sqrt 2}}{2}}}=\dfrac{3}{4}.\]
法二（利用共圆向量的数量积表达）
根据题意，有
\[\cos\angle BOC=\cos 2A=2{\cos ^2}A-1=- \dfrac{7}{9},\]
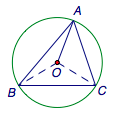
由已知
\[-\overrightarrow{OA}=\alpha\left({\overrightarrow {OB}-\overrightarrow{OA}}\right)+\beta\left({\overrightarrow{OC}-\overrightarrow{OA}}\right),\]
于是\(\left({\alpha+\beta-1}\right)\overrightarrow{OA}=\alpha\overrightarrow{OB}+\beta\overrightarrow{OC}\)．
因此
\[{\left({\alpha+\beta-1}\right)^2}\overrightarrow{OA}\cdot\overrightarrow{OA}={\alpha ^2}\overrightarrow{OB}\cdot\overrightarrow{OB}+2\alpha\beta\overrightarrow{OB}\cdot\overrightarrow{OC}+{\beta^2}\overrightarrow{OC}\cdot\overrightarrow{OC}.\]
即
\[{\left({\alpha+\beta-1}\right)^2}={\alpha^2}-\dfrac{{14}}{9}\alpha\beta+{\beta^2},\]
整理得
\[\dfrac{{32}}{9}\alpha\beta=2\left({\alpha+\beta}\right)-1.\]
又\(\alpha\beta\leqslant{\left({\dfrac{{\alpha+\beta}}{2}}\right)^2}\)，于是
\[\dfrac{9}{{32}}\left[{2\left({\alpha+\beta}\right)-1}\right]\leqslant{\left( {\dfrac{{\alpha+\beta}}{2}}\right)^2},\]
从而解得\(\alpha+\beta\geqslant\dfrac{3}{2}\)（舍去，因为\(\alpha,\beta<\dfrac{1}{2}\)）或\(\alpha+\beta\leqslant\dfrac{3}{4}\)．
而当\(\alpha=\beta=\dfrac{3}{8}\)时等号成立，因此所求最大值为\(\dfrac{3}{4}\)．
法三（利用外心的向量表达）
不妨设\(\left|{AB}\right|=1\)，\(\left|{AC}\right|=t\)，则由
\[\overrightarrow{AO}=\alpha\overrightarrow{AB}+\beta\overrightarrow{AC},\]
有
\[\overrightarrow{AO}\cdot\overrightarrow{AB}=\alpha\overrightarrow{AB}\cdot\overrightarrow{AB}+\beta\overrightarrow{AC}\cdot\overrightarrow{AB}.\]
于是\(\dfrac{1}{2}=\alpha+\dfrac{1}{3}t\beta\qquad\cdots (1)\)（注意由数量积的定义推导\(\overrightarrow{AO}\cdot\overrightarrow{AB}=\dfrac{1}{2}\)）
类似的，若两边对\(\overrightarrow{AC}\)作数量积，则有
\[\dfrac{1}{2}{t^2}=\dfrac{1}{3}t\alpha+\beta{t^2},\]
即
\[\dfrac{1}{2}t=\dfrac{1}{3}\alpha+\beta t\qquad\cdots (2)\]
由(1)(2)，得
\[t=\dfrac{{\dfrac{1}{2}-\alpha}}{{\dfrac{1}{3}\beta }}=\dfrac{{\dfrac{1}{3}\alpha }}{{\dfrac{1}{2}-\beta }},\]
从而
\[\left({\dfrac{1}{2}-\alpha}\right)\left({\dfrac{1}{2}-\beta}\right)=\dfrac{1}{9}\alpha\beta ,\]
整理得
\[\dfrac{{32}}{9}\alpha\beta=2\left({\alpha+\beta}\right)- 1.\]
以下同法二．
法四（此题的背景）
我们知道，若\(O\)为\(\triangle ABC\)内一点，则
\[{S_{\triangle OBC}}\overrightarrow{OA}+{S_{\triangle OAC}}\overrightarrow{OB}+{S_{\triangle OAB}}\overrightarrow{OC}=\overrightarrow 0,\]
特别的，若\(O\)为\(\triangle ABC\)的外心，那么就有
\[\sin 2A\overrightarrow{OA}+\sin 2B\overrightarrow{OB}+\sin 2C\overrightarrow{OC}=\overrightarrow 0.\]
换成以\(A\)为起点的，有
\[\sin 2A\overrightarrow{AO}=\sin 2B\left({\overrightarrow{AB}-\overrightarrow{AO}} \right)+\sin 2C\left({\overrightarrow{AC}-\overrightarrow{AO}}\right),\]
即
\[\overrightarrow{AO}=\dfrac{{\sin 2B}}{{\sin 2A+\sin 2B+\sin 2C}}\overrightarrow{AB}+\dfrac{{\sin 2C}}{{\sin 2A+\sin 2B+\sin 2C}}\overrightarrow{AC}.\]
于是
\[\alpha+\beta=\dfrac{{\sin 2B+\sin 2C}}{{\sin 2A+\sin 2B+\sin 2C}}=\dfrac{1}{{\dfrac{{\sin 2A}}{{\sin 2B+\sin 2C}}+1}}.\]
注意到\(\cos A=\dfrac{1}{3}\)，于是\(\sin 2A\)为定值，于是当\(\sin 2B+\sin 2C\)取得最大值时\(\alpha+\beta\)最大．
而
\[\sin 2B+\sin 2C\leqslant 2\sin\left({\dfrac{{2B+2C}}{2}}\right)=2\sin A.\]
因此\(\alpha+\beta\)的最大值为
\[\dfrac{1}{{\dfrac{{\sin 2A}}{{2\sin A}}+1}}=\dfrac{1}{{\cos A+1}}=\dfrac{3}{4}.\]