条条大路通罗马

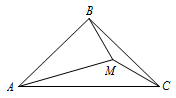
如图，在\(\triangle ABC\)中，\(\angle BAC=\angle BCA=44^\circ\)，\(M\)为\(\triangle ABC\)形内一点，使得\(\angle MCA=30^\circ\)，\(\angle MAC=16^\circ\)．求\(\angle BMC\)的度数．

答案    \(\angle BMC=150^\circ\)．

方法一：轴对称图形添加对称轴
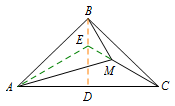作\(BD\perp AC\)于点\(D\)，延长\(CM\)交\(BD\)于点\(E\)，连接\(AE\)，则\[\angle EAM=14^\circ=\angle BAE,\angle AME=46^\circ=\angle ABE.\]所以\[\triangle ABE\cong \triangle AME,\]则\[EB=EM.\]易得\(\angle BEM=120^\circ\)，故\[\angle BMC=180^\circ-\angle BME=150^\circ.\]
方法二：构造等边三角形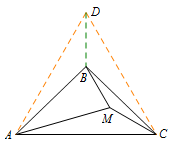以\(AC\)为边在\(\triangle ABC\)同侧作等边\(\triangle ADC\)，连接\(BD\)，则\[\angle ADB=30^\circ=\angle ACM,\angle DAB=16^\circ=\angle MAC.\]所以\[\triangle DAB\cong \triangle CAM.\]则\[AB=AM.\]从而求得\[\angle BMC=150^\circ.\]
方法三：构造等边三角形以\(AB\)为边在\(\triangle ABC\)同侧作等边\(\triangle ABD\)，则\(A,D,C\)在以\(B\)为圆心、\(BA\)为半径的圆上．连接\(DC,DM\)，则\[\angle ACD=\dfrac 12 \angle ABD=30^\circ.\]可证\[\triangle AMC \cong \triangle ADC.\]则\[AM=AD=AB,\]从而求得\[\angle BMC=\angle BMD=150^\circ.\]

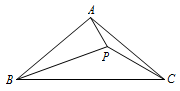
练习    在\(\triangle ABC\)中，\(\angle ABC=\angle ACB=40^\circ\)，\(P\)为形内一点，\(\angle PAC=20^\circ\)，\(\angle PCB=30^\circ\)．求\(\angle PBC\)的度数．
答案    \(\angle PBC=20^\circ\)．