每日一题[227] 向量的几何含义

2011年高考全国卷理科数学第12题（选择压轴题）：

设向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足$\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1$，$\overrightarrow{a}\cdot\overrightarrow{b}=-\dfrac{1}{2}$，$\langle\overrightarrow{a}-\overrightarrow{c},\overrightarrow{b}-\overrightarrow{c}\rangle=60^\circ$，则$\left|\overrightarrow{c}\right|$的最大值等于（        ）

A．$2$

B．$\sqrt{3}$

C．$\sqrt{2}$

D．$1$

---

正确答案是 A．

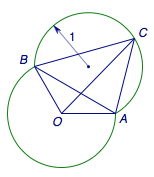
解    以$O$为起点，设向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$的终点分别为$A,B,C$．

由$\overrightarrow a\cdot\overrightarrow b=-\dfrac 12$可得$\angle{AOB}=120^\circ$，线段$AB$的长为$\sqrt 3$．

又

$$\langle\overrightarrow a-\overrightarrow c,\overrightarrow b-\overrightarrow c\rangle=\langle\overrightarrow{CA},\overrightarrow{CB}\rangle=\angle{ACB}=60^\circ,$$ 于是由定长线段的等张角线可知$C$的轨迹为过以$AB$为弦、半径为$1$的两段优弧，从而$\left|\overrightarrow{c}\right|$的最大值为$2$．

---

注    向量的加法、减法、数乘与数量积都有明确的几何意义．在向量的几何意义下，很多看似复杂的条件可以利用图形简洁明了的表达，从而大幅简化运算．

---

下面给出两道练习题．

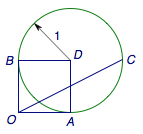
1、已知$\overrightarrow a,\overrightarrow b$为单位向量，且$\overrightarrow a\cdot \overrightarrow b=0$，若向量$\overrightarrow c$满足$\left|\overrightarrow c-\overrightarrow a-\overrightarrow b\right|=1$，则$\left|\overrightarrow c\right|$的取值范围是_______．

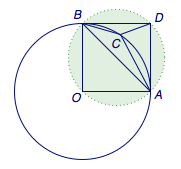
2、（2011年·辽宁·理10）若$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$均为单位向量，且$\overrightarrow{a}\cdot\overrightarrow{b}=0$,$\left(\overrightarrow{a}-\overrightarrow{c}\right)\cdot\left(\overrightarrow{b}-\overrightarrow{c}\right)\leqslant 0$，则$\left|\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\right|$的最大值为（$\qquad$）

A．$\sqrt{2}-1$

B．$1$

C．$\sqrt{2}$

D．$2$

答案    1、$\left[\sqrt 2-1,\sqrt 2+1\right]$     2、B．

提示