题目选自高中数学吧来几个题目先290楼：
已知函数\(f_t(x)=(x-t)^2-t\)，\(t\in\mathcal R\)，设\(a<b\)，\(f(x)=\begin{cases}f_a(x),&f_a(x)<f_b(x),\\f_b(x),&f_a(x)\geqslant f_b(x).\end{cases}\)若函数\(y=f(x)+x+a-b\)有四个零点，则\(b-a\)的取值范围是_______．
正确答案是\(\left(2+\sqrt 5,+\infty\right)\)．
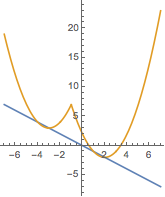
如图，\(f_t(x)\)的图象是形状恒定，顶点在直线\(y=-x\)上运动的抛物线．于是当\(a,b\)取不同值时对应的函数\(f(x)\)的图象如图．函数\(y=f(x)+x+a-b\)的零点可以视为直线\(y=-x+b-a\)与抛物线\(y=f(x)\)的交点横坐标．于是只需要两条抛物线的“交叉点”到直线\(y=-x+b-a\)的竖直距离大于\(b-a\)．
由方程\[(x-a)^2-a=(x-b)^2-b\]解得交叉点横坐标为\[x=\dfrac {a+b-1}{2},\]于是竖直距离为\[\left(\dfrac{b-a-1}{2}\right)^2+\dfrac{b-a-1}{2},\]进而通过解不等式\[\left(\dfrac{b-a-1}{2}\right)^2+\dfrac{b-a-1}{2}>b-a\]得\[b-a>2+\sqrt 5.\]