每日一题[191] 函数的位差和

2014年高考浙江卷理科数学第10题（选择压轴题）：

设函数$f_1(x)=x^2$，$f_2(x)=2\left(x-x^2\right)$，$f_3(x)=\dfrac 13\left|\sin 2\pi  x\right|$，$a_i=\dfrac{i}{99}$，$i=0,1,2,\cdots,99$．记

$$I_k=\left|f_k(a_0)-f_k(a_1)\right|+\left|f_k(a_1)-f_k(a_2)\right|+\cdots+\left|f_k(a_{98})-f_k(a_{99})\right|,k=1,2,3,$$ 则（        ）

A．$I_1<I_2<I_3$

B．$I_2<I_1<I_3$

C．$I_1<I_3<I_2$

D．$I_3<I_2<I_1$

---

正确答案是B．

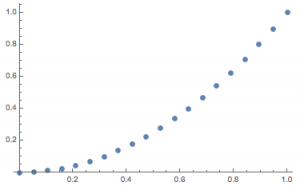
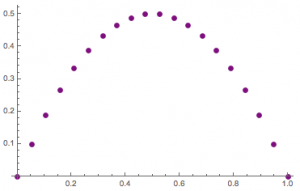
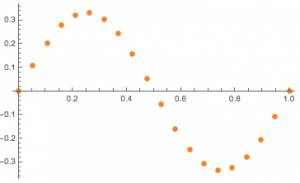
如图（为了便于观察，将原题中的$100$个点修改为了$20$个点），所求$I_k$的几何意义就是散点图的相邻点位差和．

比较散点图和连续的图象可知，如果出现“高峰”或者“低谷”，则可能有位差和的损失．而避免位差和损失的唯一方法就是将“峰顶”或者“谷底”包含在离散点集内．对于左图和中图，连续图象的位差和显然为$1$，因此很容易得到$I_1=1$，而$I_2<1$．对于右图，连续图象的位差和为$\dfrac 43$，因此虽然在转化为散点图的时候位差和有所损失，但损失极小（见注），因此$I_3\approx \dfrac 43$．

于是$I_2<I_1<1<I_3<\dfrac 43$．

---

注    实际上$I_3$位差和的损失为$4\left(\dfrac 13-\dfrac 13\sin\dfrac{49\pi}{99}\right)<\dfrac 43\left(1-\dfrac{\sqrt 3}{2}\right)<0.18$．

注    2015年高考上海卷出了一道类似的题目：http://lanqi.org/everyday/3989/．