每日一题[177] 绝对值不等式

2015年高考上海卷理科数学填空第13题：

已知函数\(f(x)=\sin x\)．若存在\(x_1,x_2,\cdots,x_m\)满足\(0\leqslant x_1<x_2<\cdots <x_m\leqslant 6\pi\)，且\(\left|f(x_1)-f(x_2)\right|+\left|f(x_2)-f(x_3)\right|+\cdots+\left|f(x_{m-1})-f(x_m)\right|=12\)（\(m\geqslant 2\)，\(m\in \mathcal N^*\)），则\(m\)的最小值为_______．

正确答案是\(8\)．

如图，取序列\[0,\dfrac{\pi}2,\dfrac{3\pi}2,\dfrac{5\pi}2,\dfrac{7\pi}{2},\dfrac{9\pi}2,\dfrac{11\pi}2,6\pi\]就得到\(m=8\)的情形．

下面证明\(m\)不可能比\(8\)更小．事实上，可以证明一个更强的命题：序列中必然包含如上所述的\(8\)个数．

直观上来说，因为要求序列数最少，所以同一个单调区间内最多存在两个点；同时，这两个点是单调区间的端点时，函数值的差的绝对值最大，所以所有点都取单调区间的端点更合适，但需要满足和为\(12\)，如图，

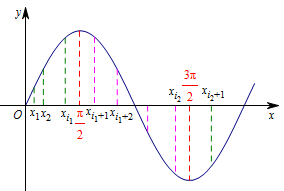
严格的推导过程如下：

如上的序列把区间\([0,6\pi]\)分成\(7\)个单调区间，不妨设\[0\leqslant x_1<\cdots<x_{i_1}\leqslant \dfrac{\pi}{2}<x_{i_1+1}<\cdots<x_{i_2}\leqslant \dfrac{3\pi}{2}<\cdots<\dfrac{11\pi}{2}<x_{i_6+1}<\cdots<x_m\leqslant 6\pi,\]则\[\begin{split}&\qquad\sum_{k=1}^{m-1}\left|f(x_k)-f(x_{k+1})\right|\\&= \left|f(x_{i_1})-f(x_1)\right|+\left|f(x_{i_1})-f(x_{i_1+1})\right|+\left|f(x_{i_1+1})-f(x_{i_2})\right|+\cdots+\left|f(x_{i_6+1})-f(x_m)\right|\\ &\leqslant \left|f(x_{i_1})-f(x_1)\right|+\left[\ \left|f(x_{i_1})-f\left(\dfrac{\pi}{2}\right)\right|+\left|f\left(\dfrac{\pi}{2}\right)-f(x_{i_1+1})\right|\ \right]+\left|f(x_{i_1+1})-f(x_{i_2})\right|\\&\qquad\qquad+\cdots+\left|f(x_{i_6+1})-f(x_m)\right|\\&=\left|f\left(\dfrac{\pi}{2}\right)-f(x_1)\right|+\left|f\left(\dfrac{\pi}{2}\right)-f\left(\dfrac{3\pi}{2}\right)\right|+\cdots+\left|f\left(\dfrac{11\pi}{2}\right)-f(x_m)\right|\\&\leqslant \left|f\left(\dfrac{\pi}{2}\right)-f(0)\right|+\left|f\left(\dfrac{\pi}{2}\right)-f\left(\dfrac{3\pi}{2}\right)\right|+\cdots+\left|f\left(\dfrac{11\pi}{2}\right)-f(6\pi)\right|\\&=12,\end{split}\]等号取得的条件为\[x_1=0,x_{i_1}=\dfrac{\pi}{2},\cdots,x_{i_6}=\dfrac{11\pi}{2},x_m=6\pi,\]即\[0,\dfrac{\pi}{2},\cdots,6\pi\in\left\{x_1,x_2,\cdots,x_m\right\},\]因此命题得证．