扑朔迷离的抛物线

2013年北京市西城区第二次模拟考试理科数学第7题：

已知正六边形\(ABCDEF\)的边长是\(2\)，一条抛物线恰好经过该正六边形相邻的四个顶点，则抛物线的焦点到准线的距离是（        ）

A．\(\dfrac{\sqrt 3}4\)

B．\(\dfrac{\sqrt 3}{2}\)

C．\(\sqrt 3\)

D．\(2\sqrt 3\)

正确答案是B．现在的问题是如果去掉“相邻的”这个条件，那么将会多出一个解（\(BCDF\)的外接抛物线的焦准距），求这个解．

注    网上能查到的版本都没有“相邻的”这一条件，不知道原卷到底是怎样的？

正确答案是\(\dfrac{\sqrt 2}4\)．

解    首先给出以下参考结论：

1、作出过四点的抛物线，这是Newton问题（见《一百个著名初等数学问题——历史和解》），有解的条件为四点构成平面上的凸包，共有两解（可能重合）；

2、过共圆四点的抛物线不仅主轴互相垂直，而且两主轴的交点就是四点的质心；

3、过共圆四点的两条抛物线的主轴方向与四边形某组对边所在直线的两条平分线方向一致．

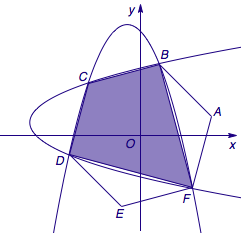
据此，可以作图如上（为了使得抛物线的主轴与坐标轴方向平行，将正六边形顺时针旋转\(15^\circ\)放置）．设抛物线的方程为\(y=ax^2+bx+c\)，则\(p=\dfrac 1{2|a|}\)．

不难证明，若抛物线\(y=ax^2+bx+c\)过点\((x_1,y_1)\)、\((x_2,y_2)\)、\((x_3,y_3)\)，则\[a=-\dfrac{y_1(x_2-x_3)+y_2(x_3-x_1)+y_3(x_1-x_2)}{(x_2-x_3)(x_3-x_1)(x_1-x_2)},\]于是将\(B\left(2\cos 75^\circ,2\sin 75^\circ\right)\)、\(C\left(2\cos 135^\circ,2\sin 135^\circ\right)\)、\(D\left(2\cos 195^\circ,2\sin 195^\circ\right)\)的坐标（即\(B\left(\dfrac{\sqrt 6-\sqrt 2}{2},\dfrac{\sqrt 6+\sqrt 2}{2}\right)\)、\(C\left(-\sqrt 2,\sqrt 2\right)\)、\(D\left(-\dfrac{\sqrt 6+\sqrt 2}{2},-\dfrac{\sqrt 6-\sqrt 2}{2}\right)\)）代入计算可得\[a=\sqrt 2,\]从而\[p=\dfrac{\sqrt 2}4.\]