2015年高考数学山东卷理科第21题（压轴题）：
设函数\(f(x)=\ln (x+1)+a\left(x^2-x\right)\)，其中\(a\in\mathcal R\)．
（1）讨论函数\(f(x)\)极值点的个数，并说明理由；
（2）若\(\forall x>0,f(x)\geqslant 0\)成立，求\(a\)的取值范围．
（1）解 根据题意，有\[f'(x)=\dfrac{1}{x+1}+a(2x-1).\]
当\(a=0\)时，函数\(f(x)\)显然没有极值点．
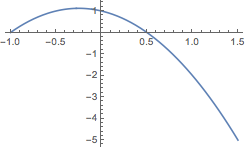
当\(a\neq 0\)时，令\(f'(x)=0\)，则有\[\dfrac 1a=-(2x-1)(x+1),\]如图．
于是函数\(f(x)\)的极值点个数为\[\begin{cases}0,&\dfrac 1a\geqslant\dfrac 98,\\1,&\dfrac 1a<0,\\2,&0<\dfrac 1a<\dfrac 98.\end{cases}\]
综上所述，函数\(f(x)\)的极值点个数为\[\begin{cases}0,&0\leqslant a\leqslant \dfrac 89,\\1,&a<0,\\2,&a>\dfrac 89.\end{cases}\]
（2）解 注意到当\(x\to 0+\)时，\(f(x)\to 0\)，于是\(f'(0+)\geqslant 0\),于是有\(a\leqslant 1\)．
又注意到当\(x\to +\infty\)时，\(f(x)<x+a(x^2-x)\)，于是有\(a\geqslant 0\)．
下面证明\(a\)在\([0,1]\)上符合题意．
当\(x\geqslant 1\)时，显然有\[f(x)\geqslant \ln (x+1)\geqslant 0;\]
当\(0\leqslant x<1\)时，有\[f(x)\geqslant \ln (x+1)+x^2-x,\]令\(g(x)=\ln (x+1)+x^2-x\)，则\[g'(x)=\dfrac{1}{x+1}+2x-1=\dfrac{2x^2+x}{x+1}\geqslant 0,\]于是\[f(x)\geqslant 0.\]
综上，\(a\)的取值范围是\([0,1]\)．
注 （1）中当\(\dfrac 1a=\dfrac 98\)时，\(f'(x)\)的零点两侧函数值的符号不会发生变号，因此不为极值点．