每日一题[115] 分类讨论

已知函数$f(x)=a{\mathrm e}^{x-1}-1$，$x\in\mathcal R$．若方程$f(x)+|x-a|=0$有且仅有两个不相等的实根，则实数$a$的取值范围为________．

---

正确的答案是$\{-1\}\cup [0,1)$．

分别考虑

$$g(x)=a{\mathrm e}^{x-1}-1+x-a,x\geqslant a$$ 和函数 $$h(x)=a{\mathrm e}^{x-1}-x+a,x<a$$ 的零点个数．

注意到

$$g'(x)=a{\mathrm e}^{x-1}+1,h'(x)=a{\mathrm e}^{x-1}-1,$$ 且当$a\leqslant 1$时$g(1)=0$．

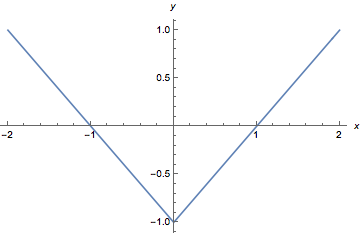
情形1    $a=0$．

此时如图，符合题意．

情形2    $a>0$．

此时$g'(x)>0$，而$h'(a)=a{\mathrm e}^{a-1}-1$有零点为$a=1$，因此需要进一步讨论．

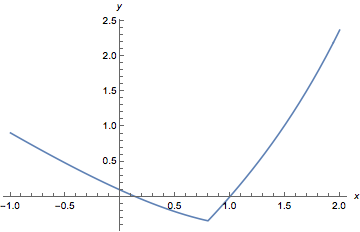
情形2.1    $0<a<1$．

此时$h'(x)<0$，因此$h(x)$单调递减，$g(x)$单调递增，而

$$g(a)=a{\mathrm e}^{a-1}-1<0,$$ 于是$g(x)$和$h(x)$各有一个零点，符合题意．

情形2.2    $a=1$．

此时与情形2.1类似，$h(x)$单调递减，$g(x)$单调递增，而

$$g(a)=a{\mathrm e}^{a-1}-1=0,$$ 于是$g(x)$有一个零点为$x=1$，$h(x)$没有零点，不符合题意．

情形2.3    $a>1$．

此时$h(x)$先递减再递增，且极小值点$x_0$满足$a{\mathrm e}^{x_0-1}-1=0$，于是可得极小值为

$$h(x_0)=a{\mathrm e}^{x_0-1}-1-x_0+a=a-x_0>0,$$ 因此$g(x)$与$h(x)$均没有零点，不符合题意．

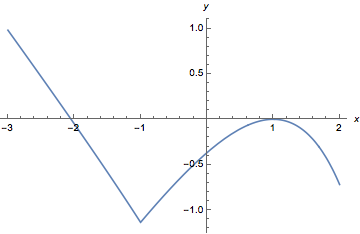
情形3    $a<0$．

此时$h'(x)<0$，而

$$g(a)=a{\mathrm e}^{a-1}-1<0,$$ 因此函数$h(x)$有一个零点．另一方面，注意到$g(a)<0$且$g(1)=0$，于是$g(x)$先递增后递减，因此只有当$x=1$为函数$g(x)$的极大值点时符合题意，此时将$x=1$代入 $$a{\mathrm e}^{x-1}+1=0$$ 解得 $$a=-1.$$

综上所述，所求实数$a$的取值范围是$\{-1\}\cup [0,1)$．

---

 

另法

当$a>0$时，将方程变形为

$${\mathrm e}^{x-1}=-\left|\dfrac 1ax-1\right|+\dfrac 1a,$$ 注意以下事实：

1、等式右边图象的“顶点”为$\left(a,\dfrac 1a\right)$，在双曲线$y=\dfrac 1x$上；

2、等式右边图象恒过点$(-1,-1)$；

3、等式左边图象与双曲线$y=\dfrac 1x$的交点为$(1,1)$，并且该点与$(-1,-1)$的连线与等式左边图象相切与$(1,1)$．

其他情形的讨论从略．