今天的题目是2015年北京市西城区高三二模数学理科的压轴题:
无穷数列\(P:a_1,a_2,\cdots,a_n,\cdots,\)满足\(a_i\in\mathcal N^*\),且\(a_i\leqslant a_{i+1}\)(\(i\in\mathcal N^*\)).对于数列\(P\),记\(T_k(P)\)(\(k\in\mathcal N^*\))表示集合\(\left\{n\left|a_n\geqslant k\right.\right\}\)中最小的数.
(1)若数列\(P:1,3,4,7,\cdots\),写出\(T_1(P),T_2(P),\cdots,T_5(P)\);
(2)若\(T_k(P)=2k-1\),求数列\(P\)前\(n\)项的和;
(3)已知\(a_{20}=46\),求\(\sum\limits_{i=1}^{20}{a_i}+\sum\limits_{j=1}^{46}{T_j(P)}\)的值.
(1)\(1,2,2,3,4\);
(2)\(\lfloor\dfrac{(n+1)^2}{4}\rfloor\);
(3)\(966\).
对于第(3)小问,标准答案中给了两种解法,分别为调整法及一般化后使用数学归纳法,解法都较为繁琐.下面给出另外两种解法.
算两次
设数列\(P\)中有\(m_i\)个\(i\),其中\(i=1,2,\cdots,46\),则\[\begin{split}\sum_{i=1}^{46}{m_i}&=20,\\\sum_{i=1}^{46}{\left(im_i\right)}&=a_1+a_2+\cdots+a_{20}.\end{split}\]于是\[\begin{split}&\quad a_1+a_2+\cdots+a_{20}+T_1(P)+T_2(P)+\cdots+T_{46}(P)\\&=\left(a_1+a_2+\cdots+a_{20}\right)+1+\left(m_1+1\right)+\cdots+\left(m_1+m_2+\cdots+m_{45}+1\right)\\&=\sum_{i=1}^{46}{im_i}+46+45m_1+44m_2+\cdots+2m_{44}+m_{45}\\&=\sum_{i=1}^{46}{\left[\left(i+46-i\right)m_i\right]}+46\\&=46\sum_{i=1}^{46}{m_i}+46\\&=46\times {20}+46\\&=966.\end{split}\]
几何解释
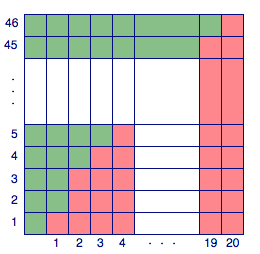
以\(P:1,3,4,5,\cdots,45,46\)为例,将\(a_i\)(\(i=1,2,\cdots,20\))用红色格子的数目表示,如图.那么\(T_j(P)\)(\(j=1,2,\cdots,46\))的几何意义是高度小于\(j\)的红色柱子的数目(将表示数列中的项的若干红色格子看成红色柱子),也就是从下往上第\(j\)行的绿色格子数.
这样就可以得到\(a_1+a_2+\cdots+a_{19}+a_{20}\)的几何意义为图中所有的红色格子按列从左向右求和,而\(T_1(P)+T_2(P)+\cdots+T_{45}(P)+T_{46}(P)\)的几何意义为图中所有的绿色格子按行从下向上求和,因此所求的和式值为\((1+20)\times 46=966\).
一般情形
一般的,若\(a_n=m\),那么\[\sum_{i=1}^{n}a_i+\sum_{j=1}^{46}{T_j(P)}=m(n+1).\]
练习题
某次测试成绩满分为\(150\)分,设\(n\)名学生的得分分别为\(a_1,a_2,\cdots,a_n\)(\(a_i\in\mathcal N,1\leqslant i\leqslant n\)),\(b_k\)(\(1\leqslant k\leqslant 150\))为\(n\)名学生中得分至少为\(k\)分的人数.记\(M\)为\(n\)名学生的平均成绩,则( )
A.\(M>\dfrac{b_1+b_2+\cdots+b_{150}}{n}\)
B.\(M=\dfrac{b_1+b_2+\cdots+b_{150}}{150}\)
C.\(M=\dfrac{b_1+b_2+\cdots+b_{150}}{n}\)
D.\(M>\dfrac{b_1+b_2+\cdots+b_{150}}{150}\)
正确答案是 C.