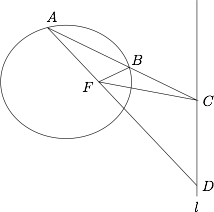
如图，已知椭圆$\Gamma$的一个焦点为$F$，与其对应的准线为$l$．直线$AB$交椭圆$\Gamma$于$A,B$两点，交准线$l$于点$C$．直线$AF$交准线$l$于点$D$．求证：$FC$平分$\angle BFD$．
分析与解 作$AM$垂直准线$l$于点$M$，作$BN$垂直准线$l$于点$N$．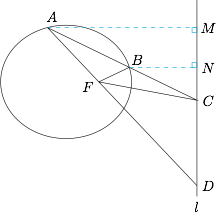
因为\[\dfrac{|FA|}{|FB|}=\dfrac{|MA|}{|NB|}=\dfrac{|CA|}{|CB|},\]故$FC$是$\triangle FAB$中$\angle AFB$的外角平分线，即$FC$平分$\angle BFD$．