每日一题[920]零点问题转化

已知函数$f(x)={\rm e}^x-ax-1$，$g(x)=\ln x-ax+a$，若存在$x_0\in (1,2)$，使得$f(x_0)g(x_0)<0$，则实数$a$的取值范围是_______．

---

正确答案是$\left(\ln 2,\dfrac{{\rm e}^2-1}2\right)$．

分析与解　考虑到$f(1)g(1)=0$，而

$$f(2)g(2)=\left({\rm e}^2-2a-1\right)\left(\ln 2-a\right),$$ 因此讨论的分界点为$a=\ln 2,\dfrac{{\rm e}^2-1}2$．

情形一　$a\leqslant \ln 2$．此时在区间$(1,2)$上，函数$f(x)$单调递增，而$f(1)>0$，因此$f(x)>0$；函数$g(x)$或者单调递增，或者先递增后递减，而$g(1),g(2)\geqslant 0$，因此$g(x)>0$．这样就有$f(x)g(x)\geqslant 0$，不符合题意．

情形二　$\ln 2<a<\dfrac{{\rm e}^2-1}2$．此时$f(2)>0$，$g(2)<0$，符合题意；

情形三　$a\geqslant \dfrac{{\rm e}^2-1}2$．此时在区间$(1,2)$上，函数$f(x)$或者单调递增，或者先递减再递增，而$f(1),f(2)\leqslant 0$，因此$f(x)<0$；函数$g(x)$单调递减(因为$g'(x)=\dfrac 1x-a<0$)，而$g(1)=0$，因此$g(x)<0$．这样就有$f(x)g(x)\geqslant 0$，不符合题意．

综上所述，实数$a$的取值范围是$\left(\ln 2,\dfrac{{\rm e}^2-1}2\right)$．

另法　也可以考虑函数

$$h(x)=f(x)g(x)=x(x-1)\left(a-\dfrac {{\rm e}^x-1}{x}\right)\left(a-\dfrac {\ln x}{x-1}\right),$$ 要使得$h(x)<0$在$x\in (1,2)$上有解，只需要$a$的值介于 $$u(x)=\dfrac {{\rm e}^x-1}x,v(x)=\dfrac {\ln x}{x-1}$$ 在某点$x_0$处的函数值之间．对它们分别求导得 $$\begin{split} u'(x)=&\dfrac {{\rm e}^x(x-1)+1}{x^2}>0,\\v'(x)=&\dfrac{1-\dfrac 1x-\ln x}{(x-1)^2}=\dfrac {\ln\frac 1x-\left(\frac 1x-1\right)}{(x-1)^2}<0,\end{split}$$ 而 $$u(2)=\dfrac 12({\rm e}^2-1),v(2)=\ln 2,$$ 它们的草图如下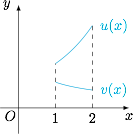：所以 $$a\in(v(2),u(2))=\left(\ln 2,\dfrac 12({\rm e}^2-1)\right).$$