每日一题[809]强强连手

已知$\triangle ABC$的周长为$2p$，求以$\triangle ABC$的某条边所在的直线为轴构成的旋转体的体积的最大值．

正确答案是$\dfrac{\pi}{12}p^3$．

分析与解　设$A,B,C$所对的边长分别为$a,b,c$．不妨设旋转体的轴过$AB$，先固定边$AB$的长$c$，则$C$点在以$A,B$为焦点，$2p-c$为长轴长的椭圆上运动．

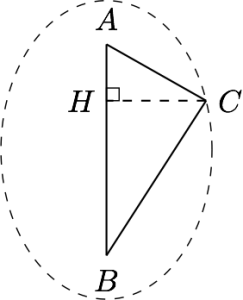
设$C$到直线$AB$的距离为$h$，则构成的旋转体 $$V=\dfrac 13\pi h^2c.$$ 易知当$a=b=p-\dfrac 12c$时，$h$取得最大值，因此有 $$V\leqslant \dfrac 13\pi\left[\left(p-\dfrac 12c\right)^2-\left(\dfrac 12c\right)^2\right]c=\dfrac{\pi}3p(p-c)c\leqslant \dfrac{\pi}3p\left(\dfrac p2\right)^2=\dfrac{\pi}{12}p^3,$$ 等号当$c=\dfrac p2$，$a=b=\dfrac 34p$时取得．因此所求的最大值为$\dfrac{\pi}{12}p^3$．