正整数$a,b$满足$1<a<b$,若关于$x,y$的方程组$\begin{cases} y=-2x+4035,\\y=|x-1|+|x-a|+|x-b|,\end{cases}$有且仅有一个实数解,则$a$的最大值为______.
正确答案是$2017$.
分析与解 函数$y=|x-1|+|x-a|+|x-b|$的图象是四段折线,折线的分界点$x=1,a,b$,各段折线的斜率分别为$-3,-1,1,3$,草图如下: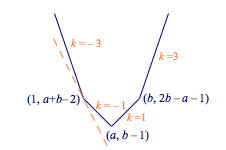
一条$k=-2$的直线与此折线只有一个公共点,所以必经过点$(1,a+b-2)$,即$$a+b-2=-2+4035=4033,$$即$a+b=4035$,又$a<b$,且$a,b$都是正整数,所以$a$的最大值为$\dfrac {4035-1}{2}=2017$.

