在平面直角坐标系中,圆$C_1:(x+1)^2+(y-6)^2=25$,圆$C_2:(x-17)^2+(y-30)^2=r^2$.若$C_2$上存在一点$P$可作一条射线与$C_1$依次交于点$A,B$,满足$|PA|=2|AB|$,则半径$r$的取值范围是_________.
分析与解 $[5,55]$.
对任意一点$P$,考虑条件的含义.
若点$P$在圆$C_1$的内部(含圆上时),一定无法作出满足条件的射线;
若点$P$在圆外时,当射线与圆相切时,一定有$|PA|>2|AB|$,所以只需要存在一条射线使得$|PA|\leqslant 2|AB|$,则点$P$满足要求.当射线过圆$C_1$的圆心时,$|PA|$有最小值$|PC_1|-r$,$|AB|$有最大值$2r$,当$|PC_1|-r\leqslant 4r$,即$|PC_1|\leqslant 5r=25$时满足条件.
所以$P$点的轨迹是以$C_1$的圆心为圆心,内外半径分别为$5$(不含)和$25$(含)的圆环.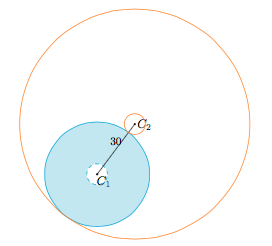
计算知$|CC_1|=30$,所以$r\in[5,55]$.

