每日一题[690]交卷顺序

阶梯教室安装的连体课桌一行坐$6$个人，考生只能从课桌两头走出考场，考生交卷时间先后不一，如果坐在里面的考生要先交卷就需要打扰别人，把一行考生中打扰别人交卷的人数视为随机变量$X$，求$X$的数学期望．

---

分析与解　设连体课桌一行坐$n$($n\geqslant 3$)个人，则随机变量$X$对应的取值为$1,2,\cdots ,n-2$．

当$n=3$时，将考生依次记为$ABC$，那么当第一个交卷的考生为$A,C$时，$X=0$，当第一个交卷的考生为$B$时，$X=1$，于是
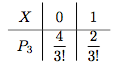当$n=4$时，将考生依次记为$ABCD$，那么当第一个交卷的考生为$A,D$时，情况转化为$n=3$的情形；当第一个交卷的考生为$B,C$时，情况转化为$n=3$的情形中每个$X$都增加$1$，比如有

$$P_4(X=1)=\dfrac 24P_3(X=0)+\dfrac 24P_3(X=1)=\dfrac {8+4}{4!}.$$ 于是有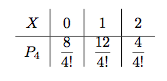进而$n=5$时，对应的分布列为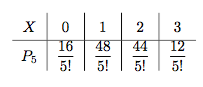而$n=6$时，对应的分布列为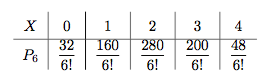于是所求的数学期望为 $$\dfrac{160+560+600+192}{6!}=\dfrac{21}{10}.$$

注　事实上，有

$$P_n(X=k)=\sum_{1\leqslant i_1<i_2<\cdots <i_k\leqslant n-2}\dfrac{\left(n-1-i_1\right)\left(n-1-i_2\right)\cdots \left(n-1-i_k\right)\cdot 2^{n-1-k}}{n!}.$$