练习题集[77]不等式提高篇

1．已知$x,y,z$是正实数，证明：$x^2+xy^2+xyz^2\geqslant 4xyz-4$．

2．设正数$a_1,a_2,\cdots ,a_n$的和为$S$，求证：$\displaystyle \sum_{i=1}^n\dfrac{a_i}{S-a_i}\geqslant \dfrac{n}{n-1}$．

3．求证：$\displaystyle \sum_{k=1}^n\dfrac{k+2}{(2k+1)(2k+3)\cdot 3^{k-1}}<\dfrac 14$．

4．求证：$\left({\rm e}^1+{\rm e}^{-1}\right)\left({\rm e}^2+{\rm e}^{-2}\right)\cdots \left({\rm e}^n+{\rm e}^{-n}\right)>\left({\rm e}^{n+1}+2\right)^{\frac n2}$．

5．已知$a,b,c\geqslant 0$，且$a+b+c=2$，求证：$\displaystyle \sum_{cyc}\dfrac{bc}{1+abc(a+b)}\leqslant 1$．

6．在$\triangle ABC$中，角$A,B,C$用弧度制度量，$a,b,c$是角$A,B,C$的对边，求证：$\dfrac{\pi}3\leqslant \dfrac{aA+bB+cC}{a+b+c}<\dfrac{\pi}2$．

7．已知$A,B,C$是$\triangle ABC$的三个内角，求证：

$$\left(\csc\dfrac A2+\csc\dfrac B2+\csc\dfrac C2\right)^2\geqslant 9+\left(\cot\dfrac A2+\cot\dfrac B2+\cot\dfrac C2\right)^2,$$ 并指明等号取得的条件．

---

参考答案

1．我们证明一个更强的命题，原不等式对$z\in\mathcal R$都成立，即对任意实数$z$，均有

$$xyz^2-4xyz+x^2+xy^2+4\geqslant 0,$$ 等价于 $$\Delta_1=16x^2y^2-4xy\left(x^2+xy^2+4\right)\leqslant 0,$$ 也即 $$xy^2-4xy+x^2+4\geqslant 0.$$ 接下来我们证明上述不等式对$y\in\mathcal R$成立，等价于 $$\Delta_2=16x^2-4x\left(x^2+4\right)\leqslant 0,$$ 也即 $$x^2+4\geqslant 4x,$$ 这显然成立．这就证明任意$x,y>0$，$z\in\mathcal R$，均有 $$x^2+xy^2+xyz^2\geqslant 4xyz-4.$$
2．不妨设$b_i=\dfrac{a_i}S$($i=1,2,\cdots ,n$)，则 $$b_1+b_2+\cdots +b_n=1,$$ 且 $$LHS=\sum_{i=1}^n\dfrac{b_i}{1-b_i},$$ 考虑到函数$f(x)=\dfrac{x}{1-x}$为下凸函数，于是 $$\sum_{i=1}^n\dfrac{b_i}{1-b_i}\geqslant nf\left(\dfrac{1}{n}\right)=\dfrac{n}{n-1},$$ 因此原不等式得证．

另解　要证不等式即

$$\sum_{i=1}^n\left(\dfrac {a_i}{S-a_i}+1\right)=\sum_{i=1}^n{\dfrac {S}{S-a_i}}\geqslant \dfrac {n^2}{n-1}.$$ 也即 $$\sum_{i=1}^n{(S-a_i)}\cdot\sum_{i=1}^n\dfrac 1{S-a_i}\geqslant n^2,$$ 由柯西不等式立得．

3．观察分母形式，考虑裂项

$$\begin{split} \sum_{k=1}^n\dfrac{k+2}{(2k+1)(2k+3)\cdot 3^{k-1}}&=\sum_{k=1}^n\left[\dfrac{1}{(2k+1)\cdot 3^{k-1}}-\dfrac{1}{(2k+3)\cdot 3^k}\right]\cdot \dfrac 34\\&=\left[\dfrac{1}{3}-\dfrac{1}{(2n+3)\cdot 3^n}\right]\cdot\dfrac 34\\&<\dfrac 14,\end{split}$$ 于是原不等式得证．

4．法一　倒序相乘
由于

$$\left({\rm e}^k+{\rm e}^{-k}\right)\left({\rm e}^{n-k+1}+{\rm e}^{-n+k-1}\right)={\rm e}^{n+1}+{\rm e}^{-n+2k-1}+{\rm e}^{n-2k+1}+{\rm e}^{-n-1}>{\rm e}^{n+1}+2,$$ 分别令$k=1,2,\cdots ,n$，各式相乘即得 $$\left({\rm e}^1+{\rm e}^{-1}\right)^2\left({\rm e}^2+{\rm e}^{-2}\right)^2\cdots \left({\rm e}^n+{\rm e}^{-n}\right)^2>\left({\rm e}^{n+1}+2\right)^{n},$$ 于是命题得证．

法二　分析通项
只需要证明

$$\left({\rm e}^{n+1}+{\rm e}^{-n-1}\right)\left({\rm e}^{n+1}+2\right)^{\frac n2}>\left({\rm e}^{n+2}+2\right)^{\frac{n+1}2},$$ 即 $$\left({\rm e}^{n+1}+{\rm e}^{-n-1}\right)^2\left({\rm e}^{n+1}+2\right)^{n}>\left({\rm e}^{n+2}+2\right)^{n+1},$$ 而 $$LHS> \left({\rm e}^{2n+2}+2\right)\left({\rm e}^{n+1}+2\right)^{n}>\left({\rm e}^{2+n}+2\right)^{n+1}=RHS,$$ 其中用到了赫尔德不等式．因此命题得证．

注　赫尔德不等式：
设$\omega_1,\omega_2,\cdots,\omega_n\geqslant 0$，且$\sum\limits_{i=1}^n{\omega_i}=1$，则对任意的$a_{ij}>0$，有

$$\left(\sum_{i=1}^m{a_{1i}}\right)^{\omega_1}\left(\sum_{i=1}^m{a_{2i}}\right)^{\omega_2}\cdots\left(\sum_{i=1}^m{a_{ni}}\right)^{\omega_n}\geqslant \sum_{j=1}^m\left(a_{1j}^{\omega_1}a_{2j}^{\omega_2}\cdots a_{nj}^{\omega_n}\right ).$$
5．只需要证明 $$1+abc(a+b)\geqslant ab+bc+ca,$$ 该不等式等价于 $$\left(ab-1\right)\left(bc+ca-1\right)\geqslant 0,$$ 又 $$ab\leqslant ab+bc=b(a+c)\leqslant \left(\dfrac{a+b+c}2\right)^2=1,$$ 类似的，有$bc+ca\leqslant 1$，因此原不等式得证．

6．不妨设$a\leqslant b\leqslant c$，则$A\leqslant B\leqslant C$，由切比雪夫不等式（或多次使用排序不等式），有

$$aA+bB+cC\geqslant \dfrac 13(a+b+c)(A+B+C),$$ 于是左边不等式得证．又 $$\begin{split} (a+b+c)(A+B+C)&=(a+b+c)A+(a+b+c)B+(a+b+c)C\\ &>2aA+2bB+2cC,\end{split}$$ 于是右边不等式得证．综上，原命题得证．

7．法一　代数变形
原不等式即

$$\left(\sum_{cyc}\csc\dfrac A2+\sum_{cyc}\cot\dfrac A2\right)\left(\sum_{cyc}\csc\dfrac A2-\sum_{cyc}\cot\dfrac A2\right)\geqslant 9,$$ 也即 $$\sum_{cyc}\dfrac{1+\cos\dfrac A2}{\sin\dfrac A2}\cdot \sum_{cyc}\dfrac{1-\cos\dfrac A2}{\sin\dfrac A2}\geqslant 9,$$ 由半角正切公式，可得 $$LHS=\sum_{cyc}\cot\dfrac{A}{4}\cdot \sum_{cyc} \tan\dfrac{A}{4},$$ 而由柯西不等式，有 $$\sum_{cyc}\cot\dfrac{A}{4}\cdot \sum_{cyc} \tan\dfrac{A}{4}\geqslant 9,$$ 因此原不等式得证．

法二　内切圆代换
如图，作$\triangle ABC$的内切圆，切点分别为$D,E,F$，且$AE=AF=x$，$BD=BF=y$，$CD=CE=z$，内切圆半径为$r$，圆心为$I$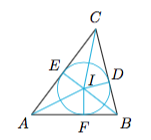．于是欲证不等式即

$$\left(\dfrac{IA}{r}+\dfrac{IB}{r}+\dfrac{IC}{r}\right)^2\geqslant 9+\left(\dfrac{x}{r}+\dfrac{y}{r}+\dfrac{z}{r}\right)^2,$$ 也即 $$(IA+IB+IC)^2\geqslant (r+r+r)^2+(x+y+z)^2,$$ 根据Minkowski不等式，有 $$\begin{split} \sqrt{(r+r+r)^2+(x+y+z)^2}&\leqslant \sqrt{r^2+x^2}+\sqrt{r^2+y^2}+\sqrt{r^2+z^2}\\ &=IA+IB+IC,\end{split}$$ 于是原不等式得证．

注　Minkowski不等式（闵可夫斯基不等式）

$$\left[\sum_{i=1}^n\left(x_i+y_i\right)^p\right]^{\frac{1}{p}}\leqslant \left(\sum_{i=1}^n{x_i^p}\right)^{\frac 1p}+\left(\sum_{i=1}^n{y_i^p}\right)^{\frac 1p},$$ 其中$x_i,y_i>0$，且$p>1$．
当$p<1$时，上述不等式的结论变为左边不小于右边．