每日一题[673]零点知多少

函数$f(x)=\sin^2[x]+\sin^2\{x\}-1$($x\in [0,100]$)的零点个数为______，函数$g(x)=[x]\cdot \{x\}-\dfrac 13x-1$($x\in [0,100]$)的零点个数为______．
(注：其中$[x]$和$\{x\}$分别表示$x$的整数部分与小数部分．)

---

分析与解　$64$，$97$．

考虑方程$f(x)=0$，即

$$\dfrac{1-\cos 2[x]}{2}+\dfrac{1-\cos 2\{x\}}{2}-1=0,$$ 也即 $$\cos 2[x]+\cos 2\{x\}=0,$$ 于是 $$2[x]\pm 2\{x\}=2k\pi +\pi ,k\in\mathcal Z,$$ 即 $$[x]\pm \{x\}=k\pi +\dfrac{\pi}2,k\in\mathcal Z.$$ 对于方程 $$[x]+\{x\}=x=k\pi +\dfrac{\pi}2,$$ 先考虑到$\dfrac{100}{\pi}\approx 31.8$，即$31.5\pi<100<32\pi$，所以当$k=0,1,2,\cdots,31$，共$32$个零点．

再考虑方程

$$[x]-\{x\}=k\pi +\dfrac{\pi}2,$$ 作出函数$y=[x]-\{x\}$的图象如下：

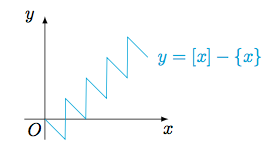易知此方程也有$32$个解（分别对应$k=0,1,2,\cdots,31$，其中每条直线$y=k\pi+\dfrac {\pi}2$与此函数有唯一交点）．

所以函数$f(x)$的零点共有$32+32=64$个．

---

最后考虑方程$g(x)=0$的解，即函数$y=[x]\cdot\{x\}$与函数$y=\dfrac 13x+1$的图象的公共点的横坐标．如图：

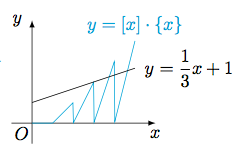
在每个区间$(k,k+1]$($k\in\mathcal N^*$且$3\leqslant k\leqslant 99$)上都有$1$个公共点，共$97$个．