平面直角坐标系$xOy$中,点$A,B,C$的坐标分别为$(a,0),(0,a),(3,4)$,点$P(x,y)$是平面内的任意一点,记$M(a)=\max\{|PA|,|PB|,|PC|\}$,则$M(a)$的最小值是______.

分析与解 先探究对于任意确定的三点,$M(a)$的最小值:
当$A,B,C$三点构成锐角或直角三角形时,$M(a)$的最小值为$\triangle ABC$的外接圆半径$r$.原因如下:
因为此时外心$D$在三角形内部(包括边界上),而任一点$P$必在$$\triangle DAB,\triangle DAC,\triangle DBC$$的其中一个三角形(包括边界)中,此时分别有$DC,DB,DA$大于等于$r$,从而有$M(a)\geqslant r$.
当$A,B,C$构成钝角三角形或共线时,$M(a)$的最小值为$\dfrac 12\max\{|AB|,|BC|,|CA|\}$.原因如下:
不妨设$A$为钝角或直角,此时$$M(a)\geqslant \dfrac 12(|PB|+|PC|)\geqslant \dfrac 12|BC|,$$当且仅当$P$为$BC$中点时取到等号.如图: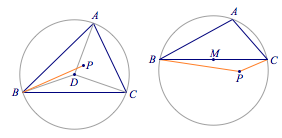 注意,始终有外接圆半径$r\geqslant \dfrac 12\max\{|AB|,|BC|,|CA|\}$.
注意,始终有外接圆半径$r\geqslant \dfrac 12\max\{|AB|,|BC|,|CA|\}$.
回到本题 因为$\overrightarrow {BC}\cdot\overrightarrow {BA}=a^2-a$,所以下面根据$a$的大小进行分类:
情形一 $a\in [0,1]$.此时$B$为钝角或直角,所以$$M(a)\geqslant\dfrac 12|AC|\geqslant \dfrac 12\sqrt{2^2+4^2}=\sqrt 5.$$
情形二 $a\in (1,3]$.此时设外心坐标$D(m,m)$,则由线段$AC$的垂直平分线方程$$y=\dfrac{a-3}4\left(x-\dfrac{a+3}2\right)+2$$可得$$m=\dfrac{25-a^2}{14-2a}=7-\left(\dfrac{7-a}2+\dfrac{12}{7-a}\right)\leqslant 7-2\sqrt 6,$$等号当且仅当$a=7-2\sqrt 6$时取得. 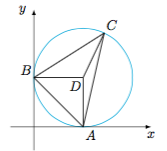 此时$\triangle ABC$外接圆的半径最小,为$7-2\sqrt 6$.
此时$\triangle ABC$外接圆的半径最小,为$7-2\sqrt 6$.
情形三 $a\in (3,+\infty)$.此时$$M(a)\geqslant \dfrac 12|AB|>\dfrac{3\sqrt 2}2>7-2\sqrt 6.$$
情形四 $a\in (-\infty,0)$.此时$$M(a)\geqslant \dfrac 12|AC|>\dfrac 52>7-2\sqrt 6.$$
因为$\sqrt 5>7-2\sqrt 6$,所以$M(a)$的最小值为$7-2\sqrt 6$.
