每日一题[571]拨云见日

已知实数$x,y$满足$x-3\sqrt{x+1}=3\sqrt{y+2}-y$，求$x+y$的最大值与最小值．

分析与解　令$a=\sqrt{x+1},b=\sqrt{y+2}$，且$a,b\geqslant 0$，则$x+y=a^2+b^2-3$，且条件变为 $$a^2-1-3a=3b-(b^2-2),$$ 即 $$\left(a-\dfrac 32\right)^2+\left(b-\dfrac 32\right)^2=\dfrac{15}2,$$ 它表示一段圆弧，如图．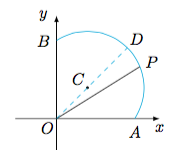
显然圆弧上的点$P$到原点的距离$OP$的最大值为 $$OD=OC+r=\dfrac{3\sqrt 2}2+\sqrt{\dfrac{15}2}=\dfrac{3\sqrt 2+\sqrt{30}}2,$$ 其中$r$为圆$C$的半径．而$OP$的最小值为 $$OA=\dfrac{3+\sqrt{21}}2.$$ 因此$x+y$的最大值为$9+3\sqrt{15}$，最小值为$\dfrac{9+3\sqrt{21}}2$．