上次在《解题的四个阶段----也谈怎样学好数学》中,我们谈了谈如何培养解题能力.那么解题能力具体包含哪些要素呢?
在我看来一个人在具体解题时,其解题能力是以下四个要素综合构成的:
力量:耐心计算,分类讨论能力;
敏捷:快速试探,精准打击能力;
智力:知识储备,模块重组能力;
运气:自强不息,相信天道佑勤.
这四要素相辅相成,不可偏废.下面就一道具体的题目,解释何谓“力量”,“敏捷”和“智力”.
2015年高考四川卷理科数学第21题(压轴题)第(2)小题:
已知函数\(f(x)=-2(x+a)\ln x+x^2-2ax-2a^2+a\),其中\(a>0\).证明:存在\(a\in (0,1)\),使得\(f(x)\geqslant 0\)在区间\((1,+\infty)\)内恒成立,且\(f(x)=0\)在区间\((1,+\infty)\)内有唯一解.
(1)解 根据已知,有\[g(x)=f'(x)=-2\ln x+2x-2-\dfrac{2a}{x}-2a,\]于是\[g'(x)=\dfrac{2}{x^2}\left(x^2-x+a\right),\]因此
当\(0<a<\dfrac 14\)时,\(g(x)\)在\(\left(0,\dfrac{1-\sqrt{1-4a}}2\right)\)上单调递增,在\(\left(\dfrac{1-\sqrt{1-4a}}2,\dfrac{1+\sqrt{1-4a}}{2}\right)\)上单调递减,在\(\left(\dfrac{1+\sqrt{1-4a}}2,+\infty\right)\)上单调递增;
当\(a\geqslant \dfrac 14\)时,\(g(x)\)在\(\mathcal R^+\)上单调递增.
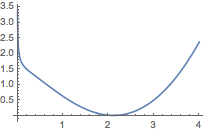
(2)力量型证明 根据题意,函数\(f(x)\)的图象应该如图所示.
考虑函数\(g(x)\),由于\(g'(1)=2a>0\),于是在\((1,+\infty)\)上\(g(x)\)单调递增.又\(g(1)=-4a<0\),\(g(+\infty)>0\),于是\(f(x)\)在\((1,+\infty)\)上先单调递减,再单调递增,有极小值点.设\(f(x)\)的极小值点为\(x=x_0\),则\[\begin{cases}-\ln x_0+x_0-1-a\left(\dfrac 1{x_0}+1\right)=0,\\-2(x_0+a)\ln x_0+x_0^2-2ax_0-2a^2+a=0,\end{cases}\]我们的目标是证明这个二元方程组有实数解,且至少有一组解满足限制条件\[x_0>1\land 0<a<1.\]
采用消元的策略,由第一个方程可得\[a=\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1},\]代入第二个方程有\[-2\left(x_0+\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}\right)\ln x_0+x_0^2-2x_0\cdot \dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}-\left(\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}\right)^2+\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1}=0,\]记该方程左边为\(\varphi (x_0)\),则\[\varphi (1)=1>0,\]且\[\begin{split}\varphi ({\rm e})&=\left({\rm e-2}\right)\left[-\dfrac{\rm e}{{\rm e}^{-1}+1}-2\dfrac {{\rm e}-2}{\left( {\rm e}^{-1}+1\right)^2}\right]\\&<0,\end{split}\]因此必然存在\(x_0\in (1,{\rm e})\),使得\(\varphi (x_0)=0\).
此时\[a=\dfrac{-\ln x_0+x_0-1}{x_0^{-1}+1},\]记该方程右边为\(\mu (x_0)\),则\[\mu' (x_0)=\dfrac{x_0^2+x_0-2-\ln x_0}{(1+x_0)^2},\]当\(x_0\in (1,{\rm e})\)时,函数\(\mu (x_0)\)单调递增(如上图),于是\[0<a<\dfrac{{\rm e}-2}{{\rm e}^{-1}+1}<1,\]因此原命题得证.
敏捷型证明 (南开中学吴剑)在“力量型证明”得到方程组后,将第一个方程变形为$$-x_0\ln x_0+x_0^2-(a+1)x_0-a=0,$$与第二个方程作差,整理得$$(x+2a)(a+\ln x -1)=0,$$因此$a=1-\ln x$,代入$$-x_0\ln x_0+x_0^2-(a+1)x_0-a=0,$$可得$$x_0^2-2x_0-1+\ln x_0=0,$$容易判断出$x_0\in (1,{\rm e})$,因此对应的$a\in (0,1)$,命题得证.
智力型证明 利用“清君侧,靖国难”的想法,可以研究函数$$g(x)=\dfrac{f(x)}{x+a}=-2\ln x+\dfrac{x^2-2ax-2a^2+a}{x+a},$$这样原问题可以转化为函数$g(x)$在$(1,+\infty)$上最小值为$0$,且最小值点$x_0$唯一.此时$g(x)$的导函数$$g'(x)=\dfrac{(x+2a)(x-1+\sqrt{1+a})(x-1-\sqrt{1+a})}{x(x+a)^2},$$于是其极小值点,亦为最小值点$$x_0=1+\sqrt{1+a},$$ 从而$$a=x_0^2-2x_0,$$因此函数$g(x)$的最小值为$$-2\ln x_0-2x_0^2+4x_0+2=0,$$从而可以估计出$x_0\in (1,{\rm e})$,因此对应的$a\in (0,1)$,命题得证.
在这个问题中,当极值点$x_0$无法用参数$a$表示时,我们会用$x_0$表示$a$,然后得到关于$x_0$的方程,通过估计$x_0$的范围反过来估计$a$的范围.在这个思路的引导下,力量型证明充分的展示了对思路信仰以及强大的计算能力.如果注意到联立方程组,通过代数变形可以大大简化$a$与$x_0$的关系,而非简单粗暴的代入消元,那么就展现了简化问题进而精准打击的能力.最后,如果有处理对数函数的知识储备,那么就可以考虑利用“清君侧”转化原来的复杂函数,通过一次求导得到极值点,然后利用与主思路一致的方式解决问题.同时,由于转化后的函数与原来的函数的零点一致,因此又可以引导出敏捷型解法.