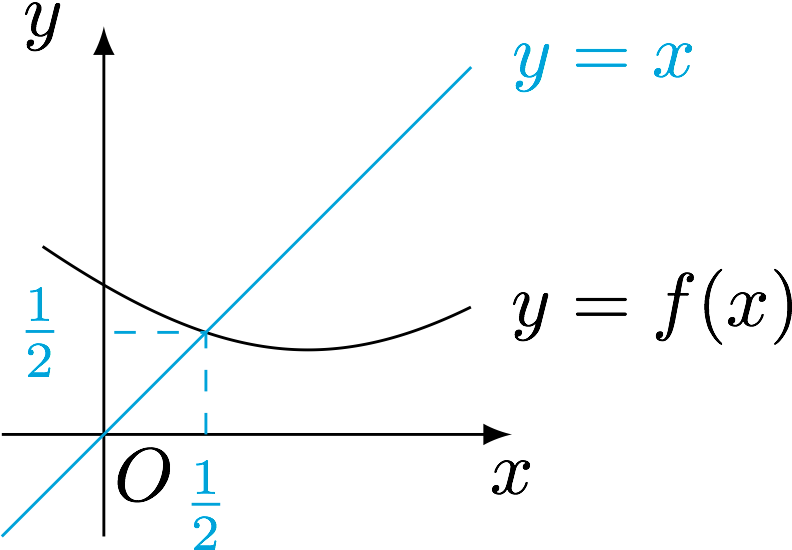已知数列$\{a_n\}$满足$a_1=1$,$a_{n+1}=\sqrt{a_n^2-2a_n+3}-1$,求证:$$a_1+a_3+a_5+\cdots +a_{2n-1}<\dfrac 12n+\dfrac 23.$$
分析 迭代函数为$f(x)=\sqrt{x^2-2x+3}-1$,解不动点方程$$x=\sqrt{x^2-2x+3}-1,$$得不动点为$x=\dfrac 12$,考虑采用不动点裂项.当然,欲证明的结论中也包含了足够的提示信息.
解 设$f(x)=\sqrt{x^2-2x+3}-1$,则$a_{n+1}=f(a_n)$.容易证明函数$f(x)$在$(-\infty,1]$上单调递减,且$f\left(\dfrac 12\right)=\dfrac 12$.
接下来用数学归纳法证明
引理 对一切正整数$n$,均有$$\sqrt 2-1\leqslant a_{2n}<\dfrac 12<a_{2n-1}\leqslant 1.$$
当$n=1$时,由于$a_1=1$,$a_2=\sqrt 2-1$,于是命题显然成立;
假设命题对$n=k$($k\in\mathcal N^*$)成立,即$$\sqrt 2-1\leqslant a_{2k}<\dfrac 12<a_{2k-1}\leqslant 1,$$则由于$f(x)$在$(-\infty ,1]$上单调递减,有$$f(\sqrt 2-1)\geqslant f(a_{2k})>f\left(\dfrac 12\right)>f(a_{2k-1})\geqslant f(1),$$即$$\sqrt 2-1\leqslant a_{2k}<\dfrac 12<a_{2k+1}\leqslant 1,$$进而$$\sqrt 2-1\leqslant a_{2k+2}<\dfrac 12<a_{2k+1}\leqslant 1,$$即命题在$n=k+1$时也成立.
综上所述,引理得证.
根据已知,可得$$a_{n+1}-\dfrac 12=\sqrt{a_n^2-2a_n+3}-\dfrac 32=\dfrac{\left(a_n-\dfrac 12\right)\left(a_n-\dfrac 32\right)}{\sqrt{a_n^2-2a_n+3}+\dfrac 32},$$于是$$\dfrac{a_{n+1}-\dfrac 12}{a_n-\dfrac 12}=\dfrac{a_n-\dfrac 32}{\sqrt{a_n^2-2a_n+3}+\dfrac 32}.$$根据引理,有$$\left|\dfrac{a_n-\dfrac 32}{\sqrt{a_n^2-2a_n+3}+\dfrac 32}\right|<\dfrac 12,$$于是可得$$\dfrac{a_{2n+1}-\dfrac 12}{a_{2n-1}-\dfrac 12}<\dfrac 14,$$从而$$\left(a_1-\dfrac 12\right)+\left(a_3-\dfrac 12\right)+\cdots +\left(a_{2n-1}-\dfrac 12\right)<\dfrac{1-\dfrac 12}{1-\dfrac 14}=\dfrac 23,$$因此原命题得证.