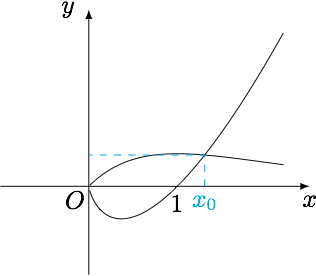
设$x>1$,$f(x)=x\ln x$,$g(x)=x{\rm e}^{-x}$,$h(x)=\min\{f(x),g(x)\}$.记$p(x)=f(x)-g(x)$的零点为$x_0$且$h(x_1)=h(x_2)$,比较$2x_0$与$x_1+x_2$的大小.
分析 函数$f(x)$的导函数$$f'(x)=1+\ln x,$$于是函数$f(x)$在$\left(0,\dfrac{1}{\rm e}\right)$上单调递减,在$\left(\dfrac{1}{\rm e},+\infty\right)$上单调递增.函数$g(x)$的导函数$$g'(x)={\rm e}^{-x}(1-x),$$于是函数$g(x)$在$(0,1)$上单调递增,在$(1,+\infty)$上单调递减.画出$f(x)$和$g(x)$的草图,可以猜测$x_1+x_2>2x_0$.
解 根据题意有$\ln x_0={\rm e}^{-x_0}$.接下来我们证明$x_1+x_2>2x_0$.
不妨设$1<x_1<x_0<x_2$.欲证明$x_1+x_2>2x_0$,只需要证明$x_2>2x_0-x_1$.考虑到$x_2$和$2x_0-x_1$均在$g(x)$的单调递减区间,因此只需要$$g(x_2)<g(2x_0-x_1),$$也即$$f(x_1)<g(2x_0-x_1),$$于是只需要证明$$\forall x_1\in (1,x_0),x_1\ln x_1<(2x_0-x_1){\rm e}^{x_1-2x_0}.$$设函数$\varphi(x)={\rm e}^{x-2x_0}\left(\dfrac{2x_0}x-1\right)-\ln x$,则只需要证明该函数在$x\in (1,x_0)$上有$\varphi(x)>0$.
函数$\varphi(x)$的导函数$$\varphi'(x)=\dfrac{{\rm e}^{x-2x_0}}{x^2}\cdot \left[-(x-x_0)^2+x_0(x_0-2)\right]-\dfrac 1x<0,$$于是有$$\varphi(x)>\varphi(x_0)=0,$$命题得证.