已知三角形\(ABC\)的顶点\(A(-2,0)\),\(B(0,4)\),欧拉线所在的方程为\(l:x+y-2=0\),则顶点\(C\)的坐标是_______.(注:三角形的欧拉线指以三角形的外心\(O\)和垂心\(H\)为端点的线段,且有\(2\overrightarrow{OG}=\overrightarrow{GH}\),其中\(G\)为三角形的重心.)
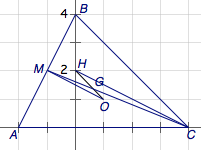
如图,\(AB\)的中点记为\(M(-1,2)\),于是线段\(AB\)的垂直平分线方程\[OM:y=-\dfrac 12x+\dfrac 32,\]与欧拉线\(l\)的方程联立可得外心\(O(1,1)\).
设顶点\(C(m,n)\),则由\(2\overrightarrow{OG}=\overrightarrow{GH}\)可得\[\overrightarrow{CH}=2\overrightarrow{OM}=(-4,2),\]于是垂心\(H(m-4,n+2)\).
垂心\(H\)的坐标满足欧拉线\(l\)的方程,因此\[m+n=4.\qquad\cdots (*)\]
同时\(AH\perp BC\),于是\[(m-2,n+2)\cdot (m,n-4)=0,\]即\[m^2-2m+n^2-2n-8=0.\qquad\cdots (**)\]
由(*)(**)解得\[m=4\land n=0,\]于是顶点\(C\)的坐标为\((4,0)\).


Pingback引用通告: 每日一题[121] 三角形的欧拉线 | Math173
图中A、B字母的位置反了。
已经修改,谢谢!