这是我在QQ群中国数学解题研究会里看到的题目:
已知$0.301029<\lg 2<0.301030$,$0.477120<\lg 3<0.477121$,求$2000^{1979}$的首位数字.
正确答案是$5$.
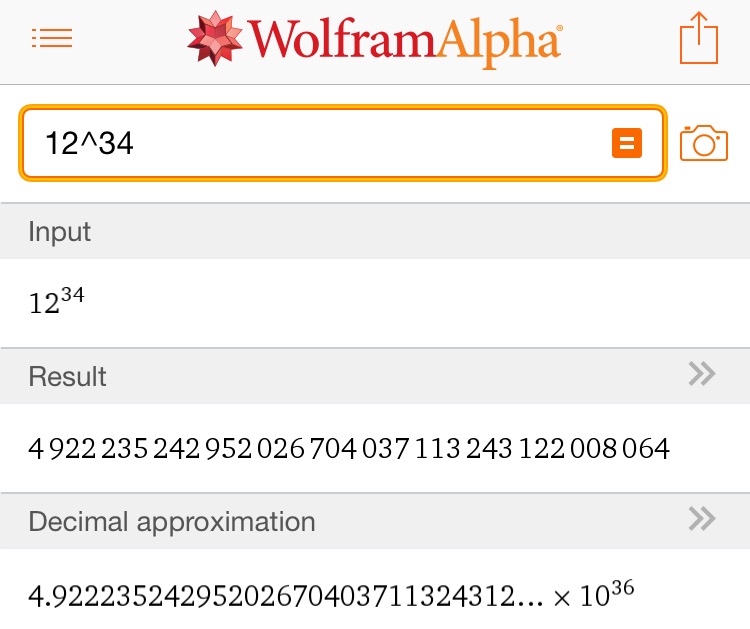
分析 利用常用对数,我们可以方便的把一个方幂写成科学记数法形式的约数.比如由于$\lg 12^{34}\approx 36.692162$,于是$$12^{34}\approx 4.922235\times 10^{36},$$其中$4.922235$是反查对数表得到的.有图有真相:
这个方法当然可以用来估计首位了,下面我们就试试看.
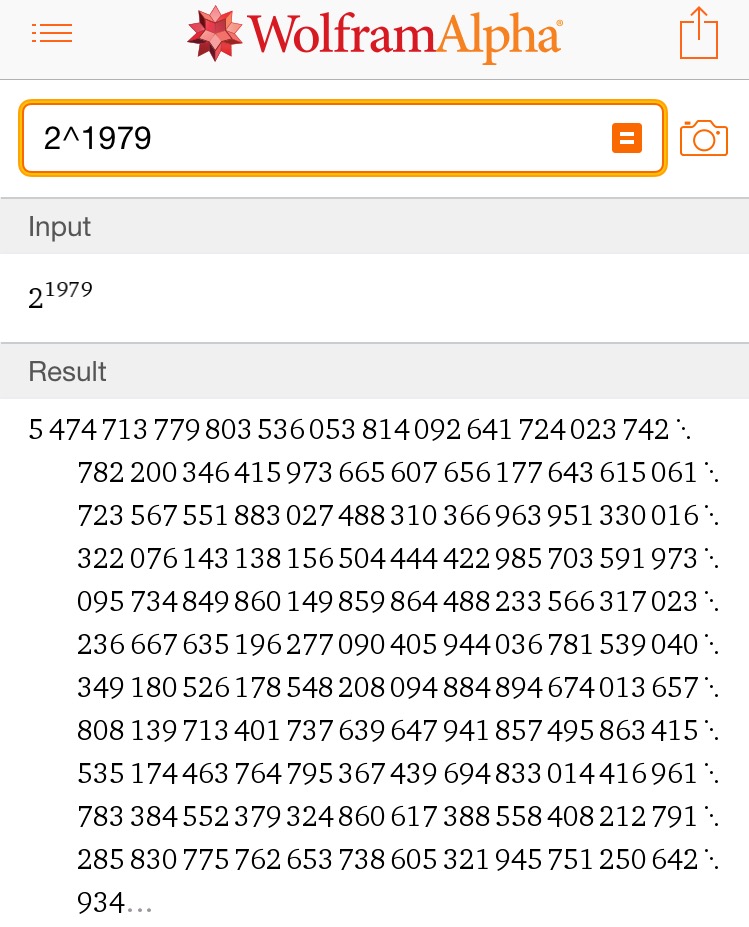
解 显然$2000^{1979}$的首位即$2^{1979}$的首位.
由于$$2^{1979}=10^{1979\lg 2}\approx 10^{595.73836}=10^{0.73836}\times 10^{595},$$其中$10^{0.73836}$为$(1,10)$内的小数,$596$是$2^{1979}$的位数.又由于$$1-\lg 2=\lg 5<0.73836<\lg 6=\lg 2+\lg 3,$$于是$$5<10^{\{1979\lg 2\}}<6.$$因此$2^{1979}$的首位为$5$,也即${2000}^{1979}$的首位是$5$.
注 $\{1979\lg 2\}$表示$1979\lg 2$的小数部分,约为$0.73836$.