每日一题[407]不战而屈人之兵

这是前几天一位同学问我的题目．

已知函数$f(x)=\ln (x+1)-a\left({\rm e}^{\frac x2}-\dfrac 14x\right)+4$无零点，求正实数$a$的取值范围．

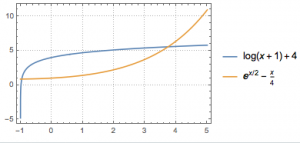
分析    这是一个很好分离变量的零点问题，先尝试分离变量，有$$a=\dfrac{\ln (x+1)+4}{{\rm e}^{\frac x2}-\dfrac 14x},$$右侧函数（设为$g(x)$）求导后的分子部分为$$\dfrac{1}{1+x}\cdot\left({\rm e}^{\frac x2}-\dfrac 14x\right)-\left[\ln (x+1)+4\right]\cdot \left(\dfrac 12{\rm e}^{\frac x2}-\dfrac 14\right),$$容易发现$x=0$为其零点，于是推测$g(0)=4$是右侧函数的一个极值．注意到函数$y=\ln (x+1)+4$是上凸函数，函数$y={\rm e}^{\frac x2}-\dfrac 14x$是下凸函数，因此所求的取值范围应该是$a>4$，如图所示．

接下来强硬的研究$g(x)$可能会比较困难，因此考虑用“不战而屈人之兵”的方式表达．

解    考虑到$f(0)=4-a$，因此$a>4$，否则$f(0)\geqslant 0$，而当$x\to -1+$（即从大于$-1$的方向逐渐趋于$-1$ ）时，$f(x)\to -\infty$（严格意义上的证明需要取点，如取$x_0=-1+\mathrm{e}^{-4}$，证明$f(x_0)<0$．也可以利用$x\to +\infty$时，$f(x)\to -\infty$，此时要注意利用$${\rm e}^x\geqslant {\rm e}^t(x-t)+{\rm e}^t,t\in\mathcal R$$进行放缩后再取点．）

下面证明当$a>4$时符合题意．

此时有$$f(x)<\ln (x+1)-4\left({\rm e}^{\frac x2}-\dfrac 14x\right)+4,$$这里用到了$$\forall x\in \mathcal R,{\rm e}^{\frac x2}-\dfrac 14x>0.$$设右侧函数为$h(x)$，则$h(x)$的导函数$$h'(x)=\dfrac{1}{x+1}-2{\rm e}^{\frac x2}+1$$是一个单调递减函数，而$h'(0)=0$，于是$h(x)$在$x=0$处取得极大值$h(0)=0$，因此$h(x)\leqslant 0$，从而$f(x)<0$，于是$f(x)$没有零点，符合题意．