已知无穷数列$\{x_n\}$的首项$x_1=\dfrac 12$,递推公式为$$x_{n+1}=\dfrac{2x_n}{x_n^2+1},n\in\mathcal N^*,$$求证:$$\dfrac{(x_1-x_2)^2}{x_1x_2}+\dfrac{(x_2-x_3)^2}{x_2x_3}+\cdots +\dfrac{(x_{n}-x_{n+1})^2}{x_nx_{n+1}}<\dfrac{5}{16}.$$
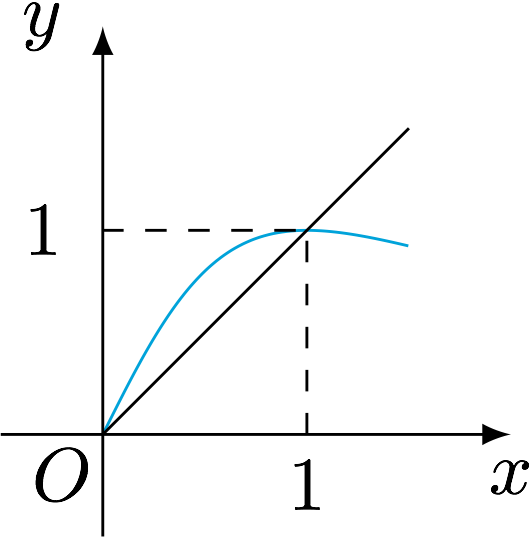
分析 利用迭代函数法研究数列,不动点为$0$和$1$,递推函数的图象如图.
可以得知$\{x_n\}$单调递增趋于$1$.由于级数通项中有因式形式为差分,因此考虑通过$\{x_n\}$的上下界进行放缩后求和(另外一种方法是利用阿贝尔求和后放缩).
解 由递推公式不难得到$x_n>0$($n\in\mathcal N^*$),又变形得$$1-x_{n+1}=\dfrac{(1-x_n)^2}{x_n^2+1}>0,$$因此$x_n<1$($n\in\mathcal N^*$).进而$$\dfrac{x_{n+1}}{x_n}=\dfrac{2}{x_n^2+1}>1,$$于是$\{x_n\}$单调递增.
接下来放缩处理和式的通项$$\dfrac{(x_{n}-x_{n+1})^2}{x_nx_{n+1}}=(x_{n+1}-x_n)\cdot\left(\dfrac{1}{x_n}-\dfrac{1}{x_{n+1}}\right),$$由于$x_1=\dfrac 12$,$x_2=\dfrac 45$,因此当$n=1$时,有$$LHS=\dfrac{(x_1-x_2)^2}{x_1x_2}=\dfrac{9}{40}<\dfrac{5}{16},$$而当$n\geqslant 2$时,有$$\dfrac{1}{x_n}-\dfrac{1}{x_{n+1}}<\dfrac 54-1=\dfrac 14,$$因此当$n\geqslant 2$时,有\[\begin{split}LHS&<\dfrac{(x_1-x_2)^2}{x_1x_2}+\dfrac 14(x_3-x_2)+\cdots +\dfrac 14(x_{n+1}-x_n)\\&=\dfrac{9}{40}+\dfrac 14(x_{n+1}-x_2)\\&<\dfrac{9}{40}+\dfrac 14\left(1-\dfrac 45\right)\\&=\dfrac{11}{40}<\dfrac{5}{16},\end{split}\]因此原命题得证.
最后留一道练习题.
已知数列$\{a_n\}$满足$a_1=1$,$a_{n+1}=\dfrac{1}{2a_n+1}$($n\in\mathcal N^*$).
(1)证明:数列$\left\{\left|a_n-\dfrac 12\right|\right\}$为单调递减数列;
(2)记$S_n$为数列$\left\{\left|a_{n+1}-a_n\right|\right\}$的前$n$项和,证明:$S_n<\dfrac 53$($n\in\mathcal N^*$).
提示 利用不动点$\dfrac 12$进行变形:$$\left|\dfrac{a_{n+1}-\frac 12}{a_n-\frac 12}\right|=\dfrac{1}{2a_n+1},$$而可以证明$\dfrac 13\leqslant a_n \leqslant 1$.对于第(2)小题,因为$$|a_{n+1}-a_n|=\left|a_{n+1}-\dfrac 12\right |+\left|a_n-\dfrac 12\right |,$$为了控制放缩的程度,尝试后将前两项单独处理,得到\[S_n<|a_2-a_1|+\left|a_2-\dfrac {1}{2}\right|+2\sum_{i=3}^{n+1}{\left|a_i-\dfrac{1}{2}\right |}\]等比放缩即得.