每日一题[56] 向量问题的图解法

今天的题目是2012年安徽高考数学理科卷的填空题．

若$\left|2\overrightarrow{a}-\overrightarrow{b}\right|\leqslant 3$，则$\overrightarrow a\cdot\overrightarrow b$的最小值是_______．

---

 正确的答案是$-\dfrac 98$．

原问题等价于

若$\left|\overrightarrow{a}-\overrightarrow{b}\right|\leqslant 3$，求$\dfrac 12\overrightarrow a\cdot\overrightarrow b$的最小值．

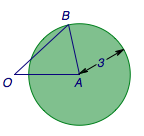
如图，设$\overrightarrow{OA}=\overrightarrow a$，$\overrightarrow{OB}=\overrightarrow b$，那么

$$\overrightarrow{AB}=\overrightarrow b - \overrightarrow a.$$ 根据题意，$\overrightarrow{AB}$的长度不超过$3$，于是$B$的可行域为以$A$为圆心、$3$为半径的圆的内部（包含边界）．

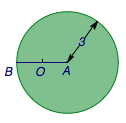
根据数量积的几何意义，使得$\overrightarrow a\cdot \overrightarrow b$取最小值的$B$位置为圆内（包括边界）的点在直线$OA$上的投影最靠左的位置．此时可得

$$\overrightarrow a\cdot \overrightarrow b=OA\cdot\left(OA-3\right)\geqslant -\dfrac 94,$$ 等号当且仅当$OA=\dfrac 32$时取得，此时对应的向量如下图所示．

下面给出一道练习题：

已知$\vec a$，$\vec b$满足$\left|\vec a\right|=5$，$\left|\vec b\right|\leqslant 1$，且$\left|\vec a-4\vec b\right|\leqslant \sqrt{21}$，则$\vec a\cdot \vec b$的最小值是_______．

参考答案    $\dfrac{25-5\sqrt{21}}{4}$．

提示    $B$的可行域为两个圆及其内部的公共部分．