已知 \(F_1\)，\(F_2\) 是椭圆和双曲线的公共焦点，\(P\) 是它们的一个公共点，且 \(\angle F_1PF_2=\dfrac{\pi}{3}\)，则椭圆和双曲线的离心率的倒数之和的最大值为（\(\qquad\)）
A．\(\dfrac{4\sqrt3}{3}\)
B．\(\dfrac{2\sqrt3}{3}\)
C．\(3\)
D．\(2\)
解 法一 设椭圆的基本量为 \(a_1\)，\(c\)，离心率为 \(e_1\)；双曲线的基本量为 \(a_2\)，\(c\)，离心率为 \(e_2\)，则题中所求即为 \[\dfrac{1}{e_1}+\dfrac{1}{e_2}=\dfrac{a_1+a_2}{c}.\cdots\cdots①\]不妨设点 \(P\) 为椭圆与双曲线在第一象限的公共点，如图所示．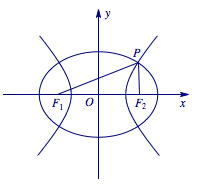
由椭圆与双曲线的定义，可得 \[\begin{cases}|PF_1|+|PF_2|=2a_1,\\|PF_1|-|PF_2|=2a_2,\end{cases}\] 两式相加，得\[a_1+a_2=|PF_1|.\cdots\cdots②\] 将②式代入①式，得 \[\dfrac{1}{e_1}+\dfrac{1}{e_2}=\dfrac{|PF_1|}{c}=2\cdot \dfrac{|PF_1|}{|F_1F_2|}.\] 在 \(\triangle PF_1F_2\) 中，我们运用正弦定理，得 \[\dfrac{|PF_1|}{|F_1F_2|}=\dfrac{\sin\angle PF_2F_1}{\sin\angle F_1PF_2}=\dfrac{2}{\sqrt3}\cdot \sin\angle PF_2F_1.\] 由此，不难得出，当 \(\angle PF_2F_1=\dfrac{\mathrm\pi}{2}\) ，可解得 \(e_1=\dfrac{\sqrt3}{3}\)，\(e_2=\sqrt3\) 时，题目所求取得最大值为 \(\dfrac{4\sqrt3}{3}\)，选项 A 正确．
法二 不妨假设椭圆与双曲线的公共焦点 \(c=1\)，\(|PF_1|=m\)，\(|PF_2|=n\)，则由法一可知，\[\dfrac{1}{e_1}+\dfrac{1}{e_2}=a_1+a_2=m.\] 在三角形 \(PF_1F_2\) 中，有余弦定理 \[|F_1F_2|^2=|PF_1|^2+|PF_2|^2-2|PF_1||PF_2|\cos\angle F_1PF_2,\] 即 \[4=m^2+n^2-mn,\] 将上式中 \(n\) 看成主元，\(m\) 看成参数，整理为二次方程 \[n^2-mn+(m^2-4)=0,\] 因此，上述方程有解，需判别式大于等于零，即 \[\Delta=m^2-4(m^2-4)\geqslant0,\] 解得 \(m\leqslant\dfrac{4\sqrt3}{3}\)，当 \(m=\dfrac{4\sqrt3}{3}\) 时， \(n=\dfrac{2\sqrt3}{3}\)，\(e_1=\dfrac{\sqrt3}{3}\)，\(e_2=\sqrt3\)，选项 A 正确．