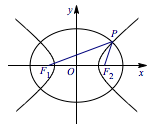
已知 \(F_1\) ,\(F_2\)是椭圆和双曲线的公共焦点,\(P\)是它们的一个公共点,且\(\angle{F_1PF_2}=\dfrac{\pi}{3}\),则椭圆和双曲线的离心率的倒数之和的最大值为____.
正确答案是\(\dfrac{4\sqrt 3}{3}\).
解 不妨设椭圆与双曲线都是焦点在$x$轴上的标准椭圆与双曲线,$P$为第一象限内的公共点,并记椭圆的半长轴长、半短轴长、离心率分别为$a_1,b_1,e_1$,双曲线的半实轴长、半虚轴长、离心率分别为$a_2,b_2,e_2$,它们的半焦距长相等,设为 $c$.
由题意知$$\begin{cases}|PF_1|+|PF_2|=2a_1,\\|PF_1|-|PF_2|=2a_2,\end{cases}$$解得$$\begin{cases}|PF_1|=a_1+a_2,\\|PF_2|=a_1-a_2.\end{cases}$$在$\triangle{PF_1F_2}$中应用余弦定理得$$\dfrac 12=\dfrac {(a_1+a_2)^2+(a_1-a_2)^2-4c^2}{2(a_1+a_2)(a_1-a_2)},$$计算得$$a_1^2+3a_2^2=4c^2.$$题目中要求的是$\dfrac {1}{e_1}+\dfrac {1}{e_2}=\dfrac {a_1}{c}+\dfrac {a_2}{c}$的最大值.设$x=\dfrac {a_1}{c},y=\dfrac {a_2}{c}$,则本题转化为已知$$x^2+3y^2=4,x>1,0<y<1,$$求$x+y$的最大值.
由柯西不等式得\[\begin{split} x+y&=1\cdot x+\dfrac {1}{\sqrt 3}\cdot {\sqrt{3}y}\\&\leqslant \sqrt{1+\dfrac 13}\cdot\sqrt{x^2+3y^2}\\&=\dfrac{4\sqrt 3}{3}.\end{split} \]当且仅当$x=3y=\sqrt 3$时取到等号.
另法(由weilew提供):
在本题中要求最大值的表达式恰为$\dfrac {a_1+a_2}{c}=\dfrac {2|PF_1|}{|F_1F_2|}$,所以也可以通过正弦定理上式等于$$\dfrac {2\sin\angle PF_2F_1}{\sin\angle F_1PF_2}=\dfrac {4}{\sqrt 3}\sin{\angle {PF_2F_1}}\leqslant \dfrac{4\sqrt 3}{3},$$当且仅当$\angle PF_2F_1=\dfrac {\pi}{2}$时取到等号.