每日一题[300] 避繁就简

已知函数$f(x)=a\ln x+\dfrac 1x+\dfrac 1{2x^2}$，$a\in\mathcal R$．

（1）讨论函数$f(x)$的单调性；

（2）证明：$(x-1)\left({\rm e} ^{-x}-x\right)+2\ln x<\dfrac 23$．

（1）解    $f(x)$的导函数 $$f'(x)=\dfrac 1{x^3}\left(ax^2-x-1\right) ,$$ 进而可得：

当$a \leqslant 0$时，函数$f(x)$在$\mathcal R^+$上单调递减；

当$a>0$时，函数$f(x)$在$\left(0,\dfrac{1+\sqrt{1+4a}}{2a} \right)$上单调递减，在$\left(\dfrac{1+\sqrt {1+4a}}{2a},+ \infty  \right)$上单调递增．

（2）证明    在（1）中取$a=2$，则可得 $$2\ln x+\dfrac 1x+\dfrac 1{2x^2}\geqslant f(1)=\dfrac 32,$$ 将其中的$x$用$\dfrac 1x$替换，可得 $$-2\ln x+x+\dfrac{x^2}2\geqslant \dfrac 32,$$ 即 $$2\ln x\leqslant x+\dfrac{x^2}2-\dfrac 32.$$

将上述不等式代入欲证明不等式的左边，有 $$\begin{split} (x-1)\left({\rm e} ^{-x}-x\right)+2\ln x &<(x-1)\cdot {\rm e} ^{-x}-x^2+x+\left(x+\dfrac{x^2}2-\dfrac 32\right)\\&=(x-1)\cdot {\rm e} ^{-x}-\dfrac{x^2}2+2x-\dfrac 32,\end{split}$$ 设右侧函数为$g(x)$，则$g(x)$的导函数 $$g'(x)=(2-x)\left({\rm e} ^{-x}+1\right),$$ 于是 $$g(x)\leqslant g(2)=\dfrac{1}{{\rm e} ^2} +\dfrac 12<\dfrac 23,$$ 因此原不等式得证．

事实上，如果不考虑利用（1）的结论．还可以尝试直接利用对数函数不等式 $$\ln x\leqslant x-1$$ 进行放缩消去对数符号： $$\begin{split}  (x-1)\left({\rm e} ^{-x}-x\right)+2\ln x&\leqslant (x-1)\left({\rm e} ^{-x}-x\right)+2(x-1)\\&=(x-1)\cdot {\rm e} ^{-x}+(2-x)(x-1).\end{split}$$

由于 $$\left(\dfrac{x-1}{{\rm e} ^{x}}\right)'=\dfrac{2-x}{{\rm e} ^x},$$ 于是其最大值为 $$\left. \left(\dfrac{x-1}{{\rm e} ^{x}}\right)\right|_{x=2}=\dfrac{1}{{\rm e} ^2},$$ 因此欲证明不等式左边 $$(x-1)\left({\rm e} ^{-x}-x\right)+2\ln x\leqslant \dfrac{1}{{\rm e} ^2}+\dfrac 14<\dfrac23.$$

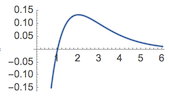
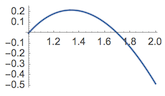
注一    可以看到不用（1）的结论可以得到更好的结果．左侧函数的最大值约为$0.218797$，如图．

注二    湖南长沙周谊老师提供了一个更简单的作法： $$\begin{split}  (x-1)\left({\rm e} ^{-x}-x\right)+2\ln x&\leqslant (x-1)\left({\rm e} ^{-x}-x\right)+2(x-1)\\&=(x-1)\cdot\left( {\rm e} ^{-x}-\dfrac{1}{\rm e} \right)+\left(2+\dfrac 1{\rm e} -x\right)(x-1)\\&<\dfrac 14\left(1+\dfrac{1}{\rm e} \right)^2&\\&<\dfrac 23.\end{split}$$