一、简单计算与证明题（每小题10分，共5小题，满分50分）
1．在空间直角坐标系中，设$O$是坐标原点，$A,B$两点的坐标分别为$\left( a_1,a_2,a_3 \right)$，$\left(b_1,b_2,b_3 \right)$．求$OA$与$OB$夹角的余弦；从$A$向$OB$作垂线交$OB$于点$P$，求点$P$的坐标．
2．记$n$个元素中取$k$个元素的组合数为$\begin{pmatrix} n\\ k \end{pmatrix}$，利用数学归纳法证明：对$n \geqslant1$，$\sum \limits _{k=0} ^{n}\begin{pmatrix} n\\ k \end{pmatrix}=2^n$．
3．确定$$\begin{cases}x+y+z=3\\x^2+y^2+z^2=3\\x^3+y^3+z^3=3\end{cases}$$的实数解．
4．设$a,b,c,d$都是正数，证明：存在三边分别等于$\sqrt {b^2+c^2}$，$\sqrt{a^2+c^2+d^2+2cd}$，$\sqrt{a^2+b^2+d^2+2ab}$的三角形，并计算该三角形的面积．
5．证明方程$$x_1^4+x_2^4+\cdots+x_{14}^4=1599$$不存在整数解．
二、解答题（满分15分）
已知正$n$边形共有$n$条对角线，它的周长等于$p$，所有对角线长度的和等于$q$，求$\dfrac qp-\dfrac pq$的值．
三、解答题（满分15分）
你收到你的信用卡的账单，信用卡的月利率是$1\%$，要求的每月最低还款额为$20$元．
（1）你决定每月还款$20$元，而且不再使用这一信用卡支付新的付款，你发现你的欠款额总是保持不变．问你收到的账单欠款是多少？
（2）如果你最初收到账单欠款是$2500$元，你希望按月等额还款$p$，且不再用信用卡支付新的付款，那么$p$为多大时正好$12$个月还清欠款？
（3）利用（1）（2）求解的启发求解满足$a_{n+1}=ra_n+b$，$a_0=c$的数列$\{a_n\}$的通项．
四、解答题（满分20分）
设$\{a,b\}$，$\{c,d\}$分别为两个矩形的长和宽，且$a<c<d<b$，$ab<cd$．证明：可将第一个矩形放入第二个矩形内部的充要条件是$$(b^2-a^2)^2 \leqslant (bd-ac)^2+(bc-ad)^2.$$
参考答案
一、简单证明和计算
1．根据已知，有$$\cos \langle \overrightarrow {OA},\overrightarrow {OB} \rangle=\dfrac {a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\cdot \sqrt{b_1^2+b_2^2+b_3^2}}.$$ 设点$P$的坐标为$k(b_1,b_2,b_3)$，由于$\overrightarrow{AP} \cdot \overrightarrow{OB}=0$，故$$\sum \limits_{i=1} ^{3} {b_i(kb_i-a_i)=0},$$解得$$k=\dfrac {\sum \limits _{i=1} ^3 {a_ib_i}}{\sum \limits_{i=1}^3 {b_i^2}},$$故点$P$的坐标为$\dfrac {\sum \limits _{i=1} ^3 {a_ib_i}}{\sum \limits_{i=1}^3 {b_i^2}}(b_1,b_2,b_3)$．
2．略．
3．因为$$\begin{split} 9&=(x+y+z)^2\\&=x^2+y^2+z^2+2(xy+yz+zx)\\&=3+2(xy+yz+zx),\end{split}$$所以$$xy+yz+zx=3=x^2+y^2+z^2,$$而$$x^2+y^2+z^2 \geqslant xy+yz+zx,$$当且仅当$x=y=z$时等号成立，所以$x=y=z=1$．
注 条件给多了．
4．如图，阴影部分即为符合题意的三角形，面积$$\begin{split}S_{ \triangle}&=(a+b)(c+d)-\dfrac 12\cdot a\cdot (c+d)-\dfrac 12\cdot bc-\dfrac 12\cdot d\cdot (a+b)\\&=\dfrac 12(ac+bc+bd).\end{split} $$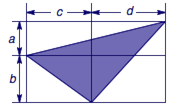 
5．若$m=2k,k \in {\mathcal Z}$，则$m\equiv 0 \pmod {16}$． 若$m=2k+1,k \in {\mathcal Z}$，由于$$\begin{split} (2k+1)^4&=16k^4+32k^3+24k^2+8k+1\\&=(16k^4+32k^3+16k^2)+8k(k+1)+1,\end{split} $$所以此时$m\equiv 1 \pmod {16}$．而$$1599\equiv 15 \pmod {16},$$故方程$x_1^4+x_2^4+\cdots+x_{14}^4=1599$不存在整数解．
二、解答题
因为$\dfrac{n(n-3)}{2}=n$，故$n=5$． 不妨设正五边形的边长为$1$，则其对角线长为$\dfrac {\sqrt 5+1}{2}$．故$\dfrac qp-\dfrac pq=1$．
三、解答题
（1）设收到账单欠款$x$元，则$$1.01(x-20)=x,$$故$$x=2020.$$
（2）设第$k$个月还款$p$元后，剩余欠款为$a_k$元，则$$\begin{split}& a_1=1.01(2500-p),\\&a_{n+1}=1.01(a_n-p)(n=1,2,\cdots,11),\\&a_{12}=0,\end{split}$$故$$p=a_{11}=1.01(a_{10}-p),$$故$$\dfrac {p}{1.01}+p=a_{10}=1.01(a_9-p),$$故$$\begin{split} \dfrac {p}{1.01^2}+\dfrac {p}{1.01}+p=a_{9}=1.01(a_8-p),\\\cdots \cdots ,\\\dfrac {p}{1.01^{11}}+\dfrac {p}{1.01^{10}}+\cdots+\dfrac {p}{1.01}+p=2500,\end{split}$$解得$$p=\dfrac {2500\times0.01 \times 1.01^{11}}{1.01^{12}-1}\approx 219.92.$$
（3）略．注意对$r$的不同取值进行分类讨论．
注一 还房贷的时候，一般是从贷款发放的下个月开始还款，所以第一次还的时候就要考虑之前一个月产生的利息了，因此房贷等额本息还款的公式与我这道题中所得到的公式略有差别．
注二 题中式子$$\dfrac {p}{1.01^{11}}+\dfrac {p}{1.01^{10}}+\cdots+\dfrac {p}{1.01}+p=2500$$直观理解也是很容易的： 第$1$个月还的$p$元都是还的本金，而第2个月还的$p$元中只有$\dfrac {p}{1.01}$元还的是本金，第3个月还的$p$元中只有$\dfrac {p}{1.01^2}$元还的是本金，以此类推． 第（3）题不需要第（1）题、第（2）题的启发即可求解，这是稍微好一些的高中生都能熟练掌握的基本问题．
四、解答题
可将第一个矩形放入第二个矩形内部的充要条件是存在$\theta \in \left(0, \dfrac {\pi}{2}\right)$，使得$$\begin{eqnarray}\begin{cases}a\sin\theta+b\cos\theta \leqslant c, \\b\sin\theta+a\cos\theta \leqslant d .\end{cases}\end{eqnarray}$$ 设$x=\cos\theta$，$y=\sin\theta$，则(1)式成立的充要条件为存在$x,y \in (0,1)$，使得$$\begin{eqnarray}\begin{cases} bx+ay \leqslant c ,\\ax+by \leqslant d ,\\x^2+y^2=1.\end{cases} \end{eqnarray}$$ 如图，设直线$\dfrac{x}{c/b}+\dfrac{y}{c/a}=1$与直线$\dfrac{x}{d/a}+\dfrac{y}{d/b}=1$与坐标轴的交点分别为$A$、$B$和$C$、$D$，两条直线的交点为$E$，则由两个不等式限制的区域为四边形$OAEC$．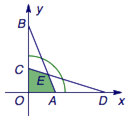 
注意到这两条直线的截距均分居$1$的两侧，因此条件组(2)有解的充要条件是交点$E$不在圆$x^2+y^2=1$的内部． 联立直线方程求得$E\left(\dfrac {bc-ad}{b^2-a^2},\dfrac {bd-ac}{b^2-a^2}\right)$，于是问题的解为$$(b^2-a^2)^2 \leqslant (bd-ac)^2+(bc-ad)^2.$$ 注 此题为第37届IMO预选题．