注 以下试题均为学生回忆的试题,不能保证真实性和正确性.欢迎读者给出解答,谢谢!
1、函数\(y=\cos\left(\pi x\right),x\in (2013,2014]\)的反函数为_______.
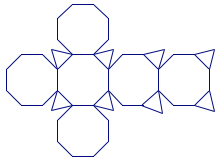
2、如图为某空间几何体的展开图,则该空间几何体共有_______条棱.
3、除\(x=1\)外,圆\(x^2+y^2=1\)与圆\((x-2)^2+(y-3)^2=1\)的另一条公切线方程为_______.
4、散点\((1.0,0.9)\),\((2.0,1.9)\),\((3.0,3.2)\)对应的回归直线方程为_______.
5、\(y=\sin\left(\omega x+\varphi\right)\)与\(y=\sin\left(2x+\dfrac{\pi}{3}\right)\)的图象关于\(x=-1\)对称,则所有可能的\(\varphi=\)_______.
6、向量\((1,2)\)绕点\((1,1)\)顺时针旋转\(45^\circ\)后所得的向量为_______.
7、\(\left|2x-y\right|+\left|x-2y\right|\leqslant 3\)所表示的平面区域面积为_______.
8、离散型随机变量\(X\)满足:\(E(X)=1\),\(D(X)=2\),则\(E\left(X^2\right)=\)_______.
9、圆\(C:x^2+y^2-2x-2y+1=0\)内位于直线\(l:y=x\tan\theta\)下方的面积为\(S\),其中\(\theta\in\left(0,\dfrac{\pi}{2}\right)\).
(1)求\(S(\theta)\)的表达式;
(2)求函数\(S(\theta)\)与函数\(S'(\theta)\)的单调性;
(3)画出\(S(\theta)\)的草图.
10、证明椭圆的光学性质.
11、已知甲袋中装有\(5\)个红球,乙袋中装有\(5\)个白球.每次从甲、乙两袋中分别随机摸一个球,同时放入对方袋中.\(n\)次操作后,甲袋中红球的个数记为\(X\).求\(X\)的分布列和数学期望.