2015年北京大学生命科学冬令营试卷数学部分

注意：所有题目均为单项选择题，共$14$小题．

1．已知函数$f(x)$是偶函数，其图象与$x$轴有$4$个交点,则$f(x)=0$的所有实根之和是（　　）

A．$1$
B．$0$
C．$2$
D．$4$

2．若$a+b=2$，则$\left(a^2-b^2\right)^2-8\left(a^2+b^2\right)$的值是（　　）

A．$-16$

B．$0$

C．$6$

D．$8$

3．方程$x^2-6x+k=0$的两个实根分别为$x_1$和$x_2$，且$x_1^2x_2^2-x_1-x_2=115$，则$x_1^2+x_2^2+8$的值是（　　）

A．$66$

B．$32$

C．$60$

D．$80$

4．当$2 \leqslant x \leqslant 3$时，二次函数$f(x)=x^2-2x-3$的最大值是（　　）

A．$-4$

B．$-3$

C．$0$

D．$1$

5．方程$x^4-y^4-4x^2+4y^2=0$表示的图形是（　　）

A．两条平行直线

B．两条相交直线

C．两条平行线与一个圆

D．两条相交直线与一个圆

6．一个梯形上下底的长度分别为$1$和$4$，两条对角线的长度分别为$3$和$4$，则梯形面积是（　　）

A．$3$

B．$4$

C．$5$

D．$6$

7．设$n$个数$x_1,x_2,\cdots,x_n$的平均数为$a$，$t<n$，$x_1,x_2,\cdots,x_t$的平均数为$b$，$x_{t+1},\cdots,x_{n}$的平均数为$c$，则有（　　）

A．$a=b+c$

B．$a=\dfrac{b+c}{2}$

C．$a=c+(b-c)\dfrac{t}{n}$

D．$a=b+(c-b)\dfrac{t}{n}$

8．设$x\in(0,\pi)$，则函数$f(x)=\left|\sqrt{1+\cos{x}}-\sqrt{1-\cos{x}}\right|$的取值范围是（　　）

A．$\left[0,\sqrt{2}\right)$

B．$\left[0,2\right)$

C．$\left[0,\sqrt{2}\right]$

D．$\left[0,2\right]$

9．外接球的半径为$1$的正四面体的棱长为（　　）

A．$\dfrac{2\sqrt{6}}{3}$

B．$\dfrac{\sqrt{6}}{2}$

C．$\dfrac{3}{2}$

D．$\dfrac{5}{4}$

10．设$f(x)$为实函数，满足$f(c)=c$的实数$c$称为$f(x)$的不动点．设$f(x)=a^x$，其中$a>0$且$a\ne 1$．若$f(x)$恰有两个互不相同的不动点，则$a$的取值范围是（　　）

A．$0<a<1$

B．$1<a<\mathrm{e}$

C．$1<a<\sqrt{\mathrm{e}}$

D．$1<a<\mathrm{e}^{\frac{1}{\mathrm{e}}}$

11．设$C_1,C_2$是平面上两个彼此外切且半径不相等的定圆，动点$C_3$与$C_1,C_2$均外切，则动点$C_3$的圆心轨迹为（　　）

A．直线

B．圆或椭圆

C．抛物线

D．双曲线的一支

12．考虑三维空间中任意给定的空间四边形$abcd$，其中$a,b,c,d$为四个顶点，四条直线段$ab,bc,cd,da$顺序首尾相连．在$a$点的内角定义为射线$ad$与射线$ab$所成的角，其补角称为$a$点的外角，其它顶点处类似．考虑这种空间四边形的外角和$X$，则有（　　）

A．$X=2\pi$

B．$X\geqslant 2\pi$

C．$X\leqslant 2\pi$

D．$X$相对于$2\pi$大小关系不确定，三种可能性都存在

13．定义函数$f(\alpha,\beta,\gamma,\delta)=\sin(\alpha-\beta)\cos(\gamma-\delta)+\sin(\alpha-\gamma)\cos(\delta-\beta)$，则此函数$f(\alpha,\beta,\gamma,\delta)$为（　　）

A．$\sin(\delta-\alpha)\cos(\beta-\gamma)$

B．$\sin(\alpha-\delta)\cos(\beta-\gamma)$

C．$\cos(\delta-\alpha )\cos(\beta -\gamma)$

D．$\cos(\alpha -\delta )\sin(\beta-\gamma)$

14．有$4$副动物拼图，每副一种颜色且各不相同，每副都固定由同一动物的$4$个不同部分（如头、身、尾、腿）组成．现在拼图被打乱后重新拼成了$4$副完整的拼图，但每一副都不是完全同色的，则符合上述条件的不同的打乱方式种数是（　　）

A．$14400$

B．$13005$

C．$24^3$

D．$63^4$

15．设有三角形$A_0B_0C_0$，做它的内切圆，三个切点确定一个新的三角形$A_1B_1C_1$，再做三角形$A_1B_1C_1$的内切圆，三个切点确定三角形$A_2B_2C_2$，以此类推，一次一次不停地做下去可以得到一个三角形序列，它们的尺寸越来越小，则最终这些三角形的极限情形是（　　）

A．等边三角形

B．直角三角形

C．与原三角形$A_0B_0C_0$相似

D．以上均不对

---

参考答案与解析

1．B．

2．A．

由题意， $$\begin{split}\left(a^2-b^2\right)^2-8\left(a^2+b^2\right)&=\left[2(a-b)\right]^2-8(4-2ab)\\&=4(a+b)^2-32\\&=-16.\end{split}$$
3．A．

考虑到一元二次方程有解，舍去$k=11$，得到$k=-11$．

4．C．

$f(x)_{\max}=f(3)=0$．

5．D．

$x^4-y^4-4x^2+4y^2=(x+y)(x-y)\left(x^2+y^2-4\right)=0$．

6．D．

平移一条对角线，将梯形的面积转化为直角三角形的面积．

7．C．

由题意， $$x_1+x_2+\cdots+x_n=na=tb+(n-t)c,$$ 所以$a=c+(b-c)\dfrac{t}{n}$．

8．A．

令$t=\cos{x}\in (-1,1)$，则 $$g(t)=\sqrt{1+t}-\sqrt{1-t}$$ 在$(-1,1)$上单调递增，故$g(t)\in \left(-\sqrt{2},\sqrt{2}\right)$，所以$f(x)=\left|g(t)\right|\in\left[0,\sqrt{2}\right)$．

也可以考虑$f(x)=\sqrt{2-2|\sin x|}=\sqrt{2-2\sin x}\in[0,\sqrt 2)$．

9．A．

棱长为$a$的正四面体的外接球半径为$\dfrac{\sqrt{6}}{4}a$，内切球半径为$\dfrac{\sqrt{6}}{12}a$（将正四面体放入正方体中考虑很容易得到这个常用的结论）．

10．D．

题意即$a^x=x$有两个根，两边取对数得$\ln a=\dfrac{\ln x}{x}$有两个不相等的根，考虑函数$g(x)=\dfrac{\ln x}{x}$，求导知$g(x)$在$(0,{\rm e}]$上单调递增，在$[\rm{e},+\infty)$上单调递减，$g(x)_{\max}=g(\rm e)=\dfrac 1{\rm e}$，且当$x\in({\rm e},+\infty)$时，有$g(x)\in\left(0,\dfrac{1}{\rm e}\right)$．所以当$\ln a\in\left(0,\dfrac 1{\rm e}\right)$时，方程有两个根，对应$f(x)$有两个不动点．

11．D．

$|C_3C_1|-|C_3C_2|=r_1-r_2\ne 0$，其中$r_1,r_2$分别表示圆$C_1,C_2$的半径．

12．B．

空间四边形的内角和与外角和的和为${4\pi}$，先考虑空间四边形的内角和$Y$，连结$bd$，如图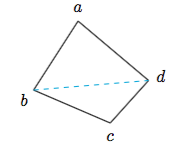： 我们用三个顶点的字母表示一个角，在$\triangle abd$与$\triangle bcd$中，有 $$\angle dab+\angle abd+\angle adb+\angle cbd+\angle cdb+\angle bcd=2\pi,$$ 所以只需要考虑$\angle abc$与$\angle abd+\angle cbd$的大小，以及$\angle adc$与$\angle adb+\angle cdb$的大小关系即可．

由三射线定理知 $$\begin{split} \cos \angle abc=&\cos \angle abd\cos \angle cbd+\sin \angle abd\sin \angle cbd \cos\theta\\\geqslant&\cos \angle abd\cos \angle cbd-\sin \angle abd\sin \angle cbd\\=&\cos(\angle abd+\angle cbd),\end{split}$$ 其中$\theta$表示二面角$a-bd-c$的大小．

于是我们得到$\angle abc\leqslant \angle abd+\angle cbd$，同理有$\angle adc\leqslant \angle adb+\angle cdb$，所以 $$Y=\angle dab+\angle abc+\angle bcd+\angle cda\leqslant 2\pi,$$ 从而$X\geqslant 2\pi$．

13．没有正确答案．

14．B．

四副拼图的颜色用$1,2,3,4$表示，四个不同的部分用$a,b,c,d$表示，第一行排$a_i$，第二行排$b_i$，第三行排$d_i$，第四行排$d_i$，则每一列都是一副完整的画．

考虑先固定第一行，确定后三行的排法即可：

在不考虑限制条件的情况下，总排法有$({\rm A}_4^4)^3$种；减去有一副图（不是只有）完整的情形，有${\rm C}_4^1({\rm A}_3^3)^3$种；再加上有两副图完整的情形，有${\rm C}_4^2({\rm A}_2^2)^3$；$\cdots$，由容斥原理知不同的打乱方式种数是 $$({\rm A}_4^4)^3-{\rm C}_4^1({\rm A}_3^3)^3+{\rm C}_4^2({\rm A}_2^2)^3-{\rm C}_4^3({\rm A}_1^1)^3+{\rm C}_4^4=13005.$$

15．A．

内切圆的顶点的对应关系如下图，为了方便，我们直接用$A_n,B_n,C_n$记$\triangle A_nB_nC_n$的三个内角（$n\in\mathbb{N}$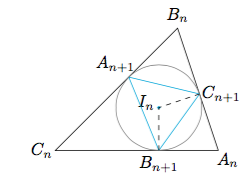）：则三角形$A_nB_nC_n$的内切圆圆心$I_n$为三角形$A_{n+1}B_{n+1}C_{n+1}$的外接圆圆心，于是有 $$A_{n+1}=\dfrac 12\angle B_{n+1}I_nC_{n+1}=\dfrac 12(\pi-A_n).$$
于是有 $$A_{n+1}-\dfrac {\pi}{3}=-\dfrac 12\left(A_n-\dfrac{\pi}{3}\right).$$ 于是有 $$A_n=\left(A_0-\dfrac{\pi}{3}\right)\cdot\left(-\dfrac 12\right)^n+\dfrac{\pi}{3},n\in\mathbb{N}.$$ 所以当$n\to+\infty$时，有$A_n\to \dfrac{\pi}{3}$，同理有$n\to +\infty,\ B_n\to\dfrac{\pi}{3},\ C_n\to\dfrac{\pi}{3}$，所以$\triangle A_nB_nC_n$的极限情形为等边三角形．

也可以直接由$2A_{n+1}+A_n=\pi$，得到$A_{n+1}=\dfrac {B_n+C_n}{2}$，从而得到这些三角形的极限情况是三个内角都相等．

点击此处下载pdf．