2010年北京大学优秀中学生夏令营试题

1、在一个双向无穷等比数列中，有三项：$\sin x,\cos x,\tan x$，求证：$\cot x$是该数列的一项．

2、求证：$\tan x^{\sin x}+\cot x^{\cos x}\geqslant 2$，其中$x\in\left(0,\dfrac{\pi}2\right)$．

3、已知三条抛物线$P_1:y=x^2+b_1x+c_1$，$P_2:y=x^2+b_2x+c_2$，$P_3:y=ax^2+bx+c$，且$P_1,P_2$与$P_3$相切．求证：$P_1,P_2$与$P_3$各自切点的连线与$P_1,P_2$的公切线平行．

4、将$1,2,\cdots ,4n$分成$n$组，每组$4$个数，满足每组中有一个数是另三个数的算术平均数，求所有可能的正整数$n$．

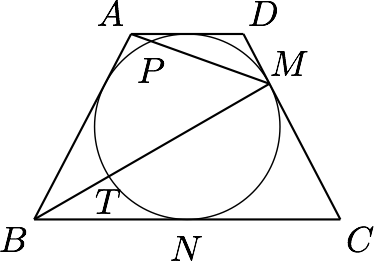
5、如图所示，圆$O$是等腰梯形$ABCD$的内切圆，$M$为切点，求$\dfrac{AM}{AP}+\dfrac{BM}{BT}$的值．

---

参考答案

1、设$\sin x,\cos x,\tan x$分别为数列中的第$m,n,p$项，注意到

$$\dfrac{\cot x}{\tan x}=\left(\dfrac{\cos x}{\sin x}\right)^2,$$ 于是$\cot x$是数列中的$p+2(n-m)$项．

2、当$\sin x\geqslant \cos x$时，有

$${\tan x}^{\sin x}+{\cot x}^{\cos x}\geqslant {\tan x}^{\cos x}+{\cot x}^{\cos x},$$ 而当$\sin x <\cos x$时，有 $${\tan x}^{\sin x}+{\cot x}^{\cos x}> {\tan x}^{\sin x}+{\cot x}^{\sin x},$$ 进而应用均值不等式即得．

3、设$P_1,P_2$的公切线为$y=kx +b_0$，则

$$(b_1-k)^2-4(c_1-b_0)=(b_2-k)^2-4(c_2-b_0)=0,$$ 解得 $$k=\dfrac {b_1+b_2}{2}-\dfrac{2(c_1-c_2)}{b_1-b_2}.$$ 设$P_1,P_2$与$P_3$的切点坐标分别为$(m_1,n_1)$，$(m_2,n_2)$，则$m_1$为方程 $$(a-1)x^2+(b-b_1)x+c-c_1=0$$ 的重根，于是判别式 $$(b-b_1)^2-4(a-1)(c-c_1)=0$$ 且$m_1=-\dfrac{b-b_1}{2(a-1)}$．化简判别式，有 $$c-c_1=\dfrac{(b-b_1)^2}{4(a-1)},$$ 从而有 $$\begin{split} \dfrac{n_2-n_1}{m_2-m_1}&=\dfrac{am_2^2+bm_2+c-am_1^2-bm_1-c}{m_2-m_1}\\ &=a(m_2+m_1)+b \\ &=a\cdot\left[-\dfrac{b-b_1}{2(a-1)}-\dfrac{b-b_2}{2(a-1)}\right]+b.\end{split}$$ 于是只需要证明 $$-a\cdot\dfrac{2b-(b_1+b_2)}{2(a-1)}+b=\dfrac{b_1+b_2}2-2\cdot\dfrac{c_1-c_2}{b_1-b_2},$$ 也即 $$\dfrac{1}{a-1}\cdot\dfrac{b-b_1+b-b_2}{2}=2\cdot\dfrac{\dfrac{(b-b_2)^2}{4(a-1)}-\dfrac{(b-b_1)^2}{4(a-1)}}{b_1-b_2},$$ 因此原命题得证．

4、$n$可以是任意正偶数．

一方面，由于

$$1+2+\cdots +4n=2n(4n+1)$$ 是$4$的倍数，因此$n$必须为偶数；

另一方面，考虑到$1,2,\cdots ,8$可以分为

$$(7,2,3,\underline{4}),(\underline{5},6,1,8),$$ 因此可以将$4n$个数先按顺序每$4$个连续的数分为一组，如 $$(1,2,3,4),(5,6,7,8),\cdots ,(4n-3,4n-2,4n-1,4n),$$ 然后将第$2k-1$组中的$8k-7$与第$2k$组中的$8k-1$交换即可，其中$k=1,2,\cdots ,\dfrac n2$．

综上，$n$为任意正偶数．

5、由切割线定理$BT\cdot BM=BN^2$，又

$$\begin{split}BM^2&=BC^2+MC^2-2BC\cdot CM\cdot \cos C\\&=4BN^2+BN^2-2\cdot 2BN\cdot BN\cdot \cos C\\&=BN^2\cdot \left(5-4\cos C\right),\end{split}$$ 两式相比即得$\dfrac{BM}{BT}=5-4\cos C$，类似的，$\dfrac{AM}{AP}=5-4\cos D$，于是所求值为$10$．

点击此处下载pdf．