2012年辽宁理科压轴题的简解

2012年高考辽宁卷理科数学第21题（压轴题）：

设\(f(x)=\ln (x+1)+\sqrt{x+1}+ax+b\)，其中\(a,b\in\mathcal R\)，\(a,b\)是常数，曲线\(y=f(x)\)与直线\(y=\dfrac 32 x\)在\((0,0)\)点相切．

（1）求\(a,b\)的值；

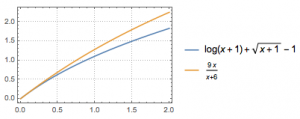
（2）证明：当\(0<x<2\)时，\(f(x)<\dfrac{9x}{x+6}\)．

解与证明    （1）根据题意，有\[f(0)=0\land f'(0)=\dfrac 32,\]解得\[a=0,b=-1.\]

（2）欲证明结论为当\(0<x<2\)时，有\[\ln (x+1)+\sqrt{x+1}-1<\dfrac{9x}{x+6},\]令\(t=\sqrt{x+1}\)，其中\(t\in\left(1,\sqrt 3\right)\)，则只需要证明\[2\ln t+t-1<\dfrac{9\left(t^2-1\right)}{t^2+5},\]我们熟知\(\forall t>1,\ln t<t-1\)，于是只需要证明\[3(t-1)<\dfrac{9\left(t^2-1\right)}{t^2+5},\]即\[\dfrac{3(t-1)^2(t-2)}{t^2+5}<0,\]这显然成立，于是命题得证．

注    第（2）问的关键在于如何处理根号和对数符号，标答给出的证明分别利用\(\sqrt{x+1}<\dfrac x2+1\)局部放缩以及整体求导处理两者．事实上，利用换元处理根号，然后利用常用函数不等式处理对数符号更加的简洁明了．