一类特殊函数的稳定点

定义    一般地，对于定义在区间$D$上的函数$y=f(x)$，若存在$x_0\in D$，使得$f(x_0)=x_0$，则称$x_0$是函数$y=f(x)$的一阶不动点，简称不动点；若存在$x_0\in D$，使$f(f(x_0))=x_0$，则称$x_0$是函数$y=f(x)$的二阶不动点，简称稳定点． 从代数角度看，一阶不动点是方程$f(x)=x$的根，二阶不动点为方程$f(f(x))=x$的根；

从几何角度看，一阶不动点是曲线$y=f(x)$与直线$y=x$的交点的横坐标，二阶不动点是曲线$y=f(x)$与曲线$x=f(y)$的交点的横坐标（曲线$y=f(x)$上关于直线$y=x$对称的点的横坐标）． 显然函数$y=f(x)$的不动点一定是函数$y=f(x)$的稳定点，但函数$y=f(x)$的稳定点不一定是不动点．如图所示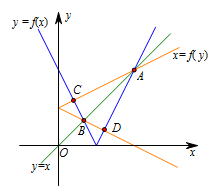： 其中点$A$，$B$的横坐标为函数$y=f(x)$的不动点和稳定点，$C$，$D$的横坐标为函数$y=f(x)$的稳定点，但不是不动点． 那什么时候稳定点与不动点是一致的呢，下面给出一个判定定理：

引理　若$f(x)$是定义域上的单调递增函数，则它的稳定点必然是它的不动点．

 设$x_0$是$f(x)$的稳定点，则$f(f(x_0))=x_0$． 若$f(x_0)>x_0$，由$f(x)$为增函数知 $$f[f(x_0)]>f(x_0)=x_0,$$ 矛盾． 若$f(x_0)<x_0$，同理可以导出矛盾．所以有 $$f(x_0)=x_0.$$

有了这个引理，如果一个函数在定义域上是单调递增的，那么稳定点就可以直接看成不动点，问题便可大大简化，如2013年四川卷理科数学第 10题（选择压轴题）：

设函数$f(x)=\sqrt{{\rm e}^x+x-a}$（$a\in\mathcal R$，$\rm e$为自然数）．若曲线$y=\sin x$ 上存在$(x_0,y_0)$ 使得$f(f(y_0))=y_0$，则$a$ 的取值范围是_______．

解    因为$f(x)\geqslant 0$，$f(f(y_0))=y_0$，所以$y_0\geqslant 0$．因为$(x_0，y_0)$是$y=\sin x$上的点，所以$y_0\in [0,1]$． 函数$f(x)=\sqrt {{\rm e}^x+x-a}$在其定义域上单调递增，所以稳定点$y_0$即为不动点，故本题转化为函数$f(x)$存在区间$[0,1]$上的不动点，即方程$f(x)=x$在$[0,1]$上有解．方程可整理为 $$a={\rm e}^x+x-x^2 (x\in [0,1]).$$ 设$g(x)={\rm e}^x+x-x^2$，则 $$g'(x)={\rm e}^x+1-2x,$$ 在$x\in [0,1]$上，${\rm e}^x\in[1,{\rm e}]$，$1-2x\in[-1,1]$，所以 $$g'(x)={\rm e}^x+1-2x\geqslant 0,$$ 所以$g(x)$在$[0,1]$上单调递增，所以 $$g(x)\in [1,{\rm e}]．$$ 故方程$a={\rm e}^x+x-x^2 (x\in [0,1])$有根，$a\in [1,{\rm e}]$．

更多关于稳定点的问题参见每日一题[35]二阶不动点．