解析几何试题的解题可以分为三步:读题构图,设参表达,消参求解,其中每一步都有各自的关键和诀窍.接下来分享的试题就体现了在“设参表达”方面的不同思路带来的解法差异.
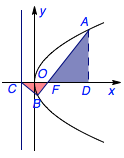
过抛物线\(y^2=2px(p>0)\)的焦点\(F\)的直线与抛物线交于\(A\),\(B\)两点,抛物线准线与\(x\)轴交于\(C\)点,若\(\angle CBF=90^\circ\),则\(|AF|-|BF|\)的值为________.
设\(A(x_1,y_1)\),\(B(x_2,y_2)\).
关键条件\(\angle CBF=90^\circ\)可以有三种转化方式:
方式一
直接用数量积表达\[\left(x_2+\frac p2,y_2\right)\cdot (x_1-x_2,y_1-y_2)=0.\]以下略.
方式二
作\(AD\)垂直\(x\)轴于\(D\),则\(\mathrm{Rt}\triangle CBF\backsim \mathrm{Rt}\triangle ADF\).于是\[\frac{CF}{BF}=\frac{AF}{DF}.\]以下略.
方式三
利用极坐标方程.设\(AB\)的方向角为\(\theta\),则\[AF=\frac{\rho}{1-\cos\theta},BF=\frac{\rho}{1+\cos\theta}.\]而\[\cos\theta=\frac{BF}{CF}=\frac{BF}p.\]从而可得\[1-\cos^2\theta=\cos\theta.\]另一方面,根据定义\[AF-BF=\frac{2p\cos\theta}{1-\cos^2\theta}=2p.\]
不难看出,由于此题和焦点相关,因此采用极坐标方程处理焦半径是最好的方法,你想到了吗?


666