2015年高考数学新课标II卷（理科）解析几何大题

2015年高考数学新课标II卷（理科）解析几何大题（第20题）：

已知椭圆$C:9x^2+y^2=m^2(m>0)$，直线$l$不过原点$O$且不平行于坐标轴，$l$与$C$有两个交点$A$、$B$，线段$AB$的中点为$M$．

（1）证明：直线$OM$的斜率与$l$的斜率的乘积为定值；

（2）若$l$过点$\left(\dfrac m3,m\right)$，延长线段$OM$与$C$交于点$P$，四边形$OAPB$能否为平行四边形？若能，求此时$l$的斜率；若不能，说明理由．

---

（1）证明    设$A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，则

$$\begin{cases}9x_1^2+y_1^2=m^2,\\9x_2^2+y_2^2=m^2,\end{cases}$$ 两式相减得 $$9\left(x_1+x_2\right)\left(x_1-x_2\right)+\left(y_1+y_2\right)\left(y_1-y_2\right)=0,$$ 即 $$\dfrac{y_1+y_2}{x_1+x_2}\cdot\dfrac{y_1-y_2}{x_1-x_2}=-9.$$ 事实上，等式左边即直线$OM$的斜率与直线$l$的斜率之积．因此原命题得证，且定值为$-9$．

（2）解    根据题意，如图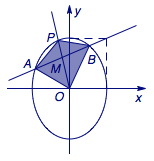． 假设存在符合题意的平行四边形$OAPB$，设$M\left(x_0,y_0\right)$，则$P\left(2x_0,2y_0\right)$，于是

$$9x_0^2+y_0^2=\dfrac 14m^2.$$ 此时根据第1小题的结论，有 $$\dfrac{m-y_0}{\dfrac m3-x_0}\cdot\dfrac{y_0}{x_0}=-9,$$ 整理得 $$3mx_0+my_0=9x_0^2+y_0^2=\dfrac 14m^2,$$ 即 $$3x_0+y_0=\dfrac 14m.$$ 由关于$x_0,y_0$的两个方程化齐次可以解得直线$l$的斜率为 $$-9\cdot\dfrac{x_0}{y_0}=4\pm\sqrt 7.$$