(理10)已知当$x\in [0,1]$时,函数$y=(mx-1)^2$的图象与$y=\sqrt x+m$的图象有且只有一个交点,则正实数$m$的取值范围是( )
A.$(0,1]\cup \left[2\sqrt 3,+\infty\right)$
B.$(0,1]\cup \left[3,+\infty\right)$
C.$\left(0,\sqrt 2\right]\cup \left[2\sqrt 3,+\infty\right)$
D.$\left(0,\sqrt 2\right]\cup \left[3,+\infty\right)$
分析与解 B.
设$f(x)=(mx-1)^2-\sqrt x-m$,$x\in [0,1]$,则\[\begin{split}f(0)&=1-m,\\f(1)&=(m-1)^2-1-m=m(m-3),\end{split}\]得到讨论分界点$m=1,3$.
情形一 $m\in (0,1)$.此时函数$f(x)$单调递减,且$f(0)\cdot f(1)<0$,因此有唯一零点,符合题意.
情形二 $m=1$.此时函数$f(x)$单调递减,且$f(0)=0$,因此有唯一零点,符合题意.
情形三 $m\in (1,3)$.此时函数$f(x)$的导函数\[f'(x)=2m(mx-1)-\dfrac{1}{2\sqrt{x}}\]是单调递增函数,因此$f(x)$或者单调,或者先单调递减再单调递增,因此在区间端点处取得最大值.而此时$f(0)<0$且$f(1)<0$,不符合题意.
情形四 $m \in \left[3,+\infty\right)$.与情形三类似,此时$f(0)<0$,$f(1)\geqslant 0$,结合$f(x)$的单调性,符合题意.
综上所述,正实数$m$的取值范围是$(0,1]\cup \left[3,+\infty\right)$.
(理15)若函数${\rm e}^xf(x)$(${\rm e}=2.71828\cdots$是自然对数的底数)在$f(x)$的定义域上单调递增,则称函数$f(x)$具有$M$性质.下列函数中所有具有$M$性质的函数的序号为________.
(1) $f(x)=2^{-x}$;(2) $f(x)=3^{-x}$;(3) $f(x)=x^3$;(4)$f(x)=x^2+2$.
分析与解 (1)(4).
(1)对于函数$f(x)=2^{-x}$,有${\rm e}^xf(x)=\left(\dfrac{\rm e}2\right)^x$在$\mathbb R$上单调递增;
(2)对于函数$f(x)=3^{-x}$,有${\rm e}^xf(x)=\left(\dfrac{\rm e}3\right)^x$在$\mathbb R$上单调递减;
(3)对于函数$f(x)=x^3$,有\[\left({\rm e}^xf(x)\right)'={\rm e}^x\left(x^3+3x^2\right)={\rm e}^x\cdot x^2\left(x+3\right),\]因此在$(-\infty,-3)$上,函数${\rm e}^xf(x)$单调递减;
(4)对于函数$f(x)=x^2+2$,有\[\left({\rm e}^xf(x)\right)'={\rm e}^x\left(x^2+2+2x\right)={\rm e}^x\left[(x+1)^2+1\right]>0,\]因此函数${\rm e}^xf(x)$在$\mathbb R$上单调递增.
综上所述,具有$M$性质的函数的序号是(1)(4).
(理20)已知函数$f(x)=x^2+2\cos x$,$g(x)={\rm e}^x(\cos x-\sin x+2x-2)$,其中${\rm e}=2.71828\cdots$是自然对数的底数.
(1) 求曲线$y=f(x)$在点$(\pi ,f(\pi))$处的切线方程;
(2) 令$h(x)=g(x)-af(x)$($a\in\mathbb R$),讨论$h(x)$的单调性并判断有无极值,有极值时求出极值.
分析与解 (1) 函数$f(x)$的导函数\[f'(x)=2x-2\sin x,\]于是$f(\pi)=\pi^2-2$,$f'(\pi)=2\pi$,所求的切线方程为\[y=2\pi(x-\pi)+\pi^2-2,\]也即$y=2\pi x-\pi^2-2$.
(2) 根据题意,有\[h(x)={\rm e}^x(\cos x-\sin x+2x-2)-ax^2-2a\cos x,\]其导函数\[h'(x)=2\left({\rm e}^x-a\right)\left(x-\sin x\right).\]由于\[\left(x-\sin x\right)'=1-\cos x,\]于是该函数单调递增,有唯一零点$x=0$.这样就得到了讨论分界点$a=0,1$.
情形一 $a\leqslant 0$.此时函数$h(x)$在$(-\infty,0)$上单调递减,在$(0,+\infty)$上单调递增,在$x=0$处取得极小值$-1-2a$.
情形二 $0<a<1$.此时函数$h(x)$在$(-\infty,\ln a)$上单调递增,在$(\ln a,0)$上单调递减,在$(0,+\infty)$上单调递增,在$x=\ln a$处取得极大值$$2a\ln a-2a-a\ln^2a-a\sin\ln a-a\cos\ln a,$$在$x=0$处取得极小值$-1-2a$.
情形三 $a=1$.此时函数$h(x)$在$\mathbb R$上单调递增,没有极值.
情形四 $a>1$.此时函数$h(x)$在$(-\infty,0)$上单调递增,在$(0,\ln a)$上单调递减,在$(\ln a,+\infty)$上单调递增,在$x=0$处取得极大值$-1-2a$,在$x=\ln a$处取得极小值$$2a\ln a-2a-a\ln^2a-a\sin\ln a-a\cos\ln a.$$
(理21)在平面直角坐标系$xOy$中,椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的离心率为$\dfrac{\sqrt 2}2$,焦距为$2$.
(1)求椭圆$E$的方程;
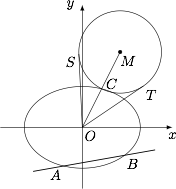
(2) 如图,动直线$l:y=k_1x-\dfrac{\sqrt 3}2$交椭圆$E$于$A,B$两点,$C$是椭圆$E$上一点,直线$OC$的斜率为$k_2$,且$k_1k_2=\dfrac{\sqrt 2}4$.$M$是线段$OC$延长线上一点,且$|MC|:|AB|=2:3$,圆$M$的半径为$|MC|$,$OS,OT$是圆$M$的两条切线,切点分别为$S,T$.求$\angle SOT$的最大值,并求取得最大值时直线$l$的斜率.
 分析与解 (1) 椭圆$E$的方程为$\dfrac{x^2}2+y^2=1$.
分析与解 (1) 椭圆$E$的方程为$\dfrac{x^2}2+y^2=1$.
(2) 设$\angle SOM=\theta$,则$\angle SOT=2\theta$,且\[\sin\theta=\dfrac{|MC|}{|OM|}=\dfrac{\dfrac 23|AB|}{|OC|+\dfrac 23|AB|}=\dfrac{2}{2+3\cdot \dfrac{|OC|}{|AB|}}.\]联立直线$l$与椭圆$E$的方程,可得\[\left(\dfrac 12+k_1^2\right)x^2-\sqrt 3k_1x-\dfrac 14=0,\]因此\[|AB|=\sqrt{1+k_1^2}\cdot \dfrac{\sqrt{4k_1^2+\dfrac 12}}{\dfrac 12+k_1^2}.\]联立直线$y=k_2x$与椭圆$E$的方程,可得\[\left(\dfrac 12+k_2^2\right)x^2=1,\]因此\[|OC|=\sqrt{1+k_2^2}\cdot \dfrac{1}{\sqrt{\dfrac 12+k_2^2}}=\dfrac{\sqrt{k_1^2+k_1^2k_2^2}}{\sqrt{\dfrac 12k_1^2+k_1^2k_2^2}}=\dfrac{\sqrt{k_1^2+\dfrac 18}}{\sqrt{\dfrac 12k_1^2+\dfrac 18}}.\]这样就有\[\begin{split}\dfrac{|OC|}{|AB|}&=\dfrac{\sqrt{k_1^2+\dfrac 18}}{\sqrt{\dfrac 12k_1^2+\dfrac 18}}\cdot \dfrac{\dfrac 12+k_1^2}{\sqrt{1+k_1^2}\cdot \sqrt{4k_1^2+\dfrac 12}}\\&=\dfrac{1}{\sqrt 2}\cdot \dfrac{k_1^2+\dfrac 12}{\sqrt{k_1^2+\dfrac 14}\cdot \sqrt{k_1^2+1}}\\&=\dfrac{1}{\sqrt 2}\cdot \sqrt {1-\dfrac{1}{4k_1^2+\dfrac{1}{k_1^2}+5}}\\&\geqslant \dfrac{1}{\sqrt 2}\cdot \sqrt{1-\dfrac{1}{2\sqrt{4k_1^2\cdot \dfrac{1}{k_1^2}}+5}}\\&=\dfrac 23,\end{split}\]等号当且仅当$k_1^2=\dfrac 12$时取得.因此$\sin\theta$的最大值为\[\dfrac{2}{2+3\cdot \dfrac 23}=\dfrac 12,\]继而$\angle SOT$的最大值为$\dfrac{\pi}3$,此时直线$l$的斜率为$\pm \dfrac{\sqrt 2}2$.

