12．几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案： 已知数列$1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,\cdots ,$其中第一项是$2^0$，接下来的两项是$2^0,2^1$，再接下来的三项是$2^0,2^1,2^2$，依此类推．求满足如下条件的最小整数$N$：$N>100$且该数列的前$N$项和为$2$的整数幂．那么该款软件的激活码是 ( )
A．$440$
B．$330$
C．$220$
D．$110$
正确答案为A.
分析与解 分段考虑数列\[\begin{split}&1,\\&1,2,\\&1,2,4,\\&\cdots,\\&1,2,\cdots,2^{k-1},\\&\cdots,\end{split}\]该数列的前$1+2+\cdots+k=\dfrac {k(k+1)}2$项的和为$$S\left(\dfrac {k(k+1)}2\right)=1+(1+2)+\cdots+(1+2+\cdots+2^{k-1})=2^{k+1}-k-2.$$要使得$\dfrac {k(k+1)}2>100$，有$k\geqslant 14$，此时$k+2<2^{k+1}$，所以$k+2$是之后的等比数列$1,2,\cdots,2^{k}$的部分和，也即$$k+2=1+2+\cdots+2^{s-1}=2^s-1,$$所以$k=2^s-3\geqslant 14$，最小的$s=5$，此时$k=2^5-3=29$，对应最小的满足条件的$$N=\dfrac {29\cdot 30}2+5=440.$$
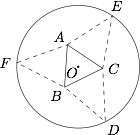
16．如图，圆形纸片的圆心为 $O$，半径为 $5\;\mathrm{cm}$，该纸片上的等边三角形 $ABC$ 的中心为 $O$．$D,E,F$ 为圆 $O$ 上的点，$\triangle DBC,\triangle ECA,\triangle FAB$ 分别是以 $BC,CA,AB$ 为底边的等腰三角形，沿虚线剪开后，分别以 $BC,CA,AB$ 为折痕折起 $\triangle DBC,\triangle ECA,\triangle FAB$，使得 $D,E,F$ 重合，得到三棱锥．当 $\triangle ABC$ 的边长变化时，所得三棱锥体积(单位：$\mathrm{cm}^3$)的最大值为_______．
分析与解 连接 $OD$，交 $BC$ 于 $H$，如图
设 $BC=2x$，则 $0<2x<5\sqrt 3$， $OH=\dfrac {x}{\sqrt 3}$，$DH=5-\dfrac {x}{\sqrt 3}$ ．所以\[\begin{split}V&=\dfrac 13 \cdot \dfrac {\sqrt 3}{4}\cdot (2x)^2\cdot \sqrt {\left(5-\dfrac {x}{\sqrt 3}\right)^2- \left(\dfrac {x}{\sqrt 3}\right)^2}\\&=\dfrac {\sqrt 3}{3}\cdot x^2 \cdot \sqrt {25-\dfrac {10x}{\sqrt 3}}\\&=\dfrac {\sqrt 3}{3}\cdot \sqrt { x\cdot x\cdot x\cdot x\cdot \dfrac {10}{\sqrt 3}\left(\dfrac {5\sqrt 3}{2}-x\right)}\\&=\dfrac {\sqrt 3}{3}\cdot \sqrt { x\cdot x\cdot x\cdot x\cdot \dfrac {5}{2\sqrt 3}\left( {10\sqrt 3} -4x\right)}\\&\leqslant \dfrac {\sqrt 3}{3}\cdot \sqrt {\dfrac {5}{2\sqrt 3}\left(\dfrac {10\sqrt 3}{5} \right)^5} \\&= 4\sqrt {15}.\end{split}\]当$x=2\sqrt 3$时取等号．
20．已知椭圆 $C:\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1(a>b>0)$，四点 $P_1\left(1,1\right)$、$P_2\left(0,1\right)$、$P_3\left(-1,\dfrac {\sqrt 3}{2}\right)$、$P_4\left(1, \dfrac {\sqrt 3}{2}\right)$ 中恰有三点在椭圆 $C$ 上．
(1)求 $C$ 的方程；
(2)设直线 $l$ 不经过 $P_2$ 点且与 $C$ 相交于 $A,B$ 两点．若直线 $P_2A$ 与直线 $P_2B$ 的斜率的和为 $-1$ ，证明： $l$ 过定点．
分析与解 (1)根据椭圆的对称性，可知 $P_2,P_3,P_4$ 在椭圆 $C$ 上，所以椭圆方程为 $\dfrac{x^2}{4}+y^2=1$．
(2)将坐标系向上平移一个单位，如图
椭圆方程化为 $$C':\dfrac{x'^2}{4}+(y'+1)^2=1\;,\mbox{即}\;\dfrac14x'^2+y'^2+2y'=0,$$ 设直线 $l$ 对应的直线 $l'$ 为 $mx'+ny'=1$，则化齐次联立，得 $$\dfrac14x'^2+y'^2+2y'(mx'+ny')=0,$$ 整理得 $$(2n+1)y'^2+2mx'y'+\dfrac14x'^2=0,$$ 结合两直线斜率之和为 $-1$，得 $$2m=2n+1,\;\mbox{即}\;2m-2n=1,$$ 所以直线 $l'$ 恒过点 $Q'(2,-2)$，在原坐标系中，直线 $l$ 过点 $Q(2,-1)$．
21．已知函数\(f(x)=a{\rm e}^{2x}+(a-2){\rm e}^{x}-x\)．
(1)讨论\(f(x)\)的单调性；
(2)若\(f(x)\)有两个零点，求\(a\)的取值范围．
分析与解 (1)\(f(x)\)的导函数为\[f'(x)=2a{\rm e}^{2x}+(a-2){\rm e}^{x}-1=(a{\rm e}^{x}-1)(2{\rm e}^{x}+1).\]
当\(a\leqslant 0\)时，\(f'(x)<0\)；
当\(a>0\)时，在区间\(\left(-\infty,\ln\dfrac{1}{a}\right)\)上有\(f'(x)<0\)，在区间\(\left(\ln\dfrac{1}{a},+\infty\right)\)上有\(f'(x)>0\)．
综上，当\(a\leqslant 0\)时，\(f(x)\)在\(\mathbb R\)上单调递减；
当\(a>0\)时，\(f(x)\)在\(\left(-\infty,\ln\dfrac{1}{a}\right)\)上单调递减，在\(\left(\ln\dfrac{1}{a},+\infty\right)\)上单调递增．
(2)令\(f(x)=0\)，即\(a{\rm e}^{2x}+(a-2){\rm e}^{x}-x=0\)，所以有\[a=\dfrac{2{\rm e}^{x}+x}{{\rm e}^{2x}+{\rm e}^{x}}.\]于是函数\(f(x)\)有两个零点，即\(y=a\)与\(g(x)=\dfrac{2{\rm e}^{x}+x}{{\rm e}^{2x}+{\rm e}^{x}}\)的图象有两个交点．
\(g(x)\)的导函数为\(g'(x)=-\dfrac{(2{\rm e}^{x}+1)({\rm e}^{x}+x-1)}{{\rm e}^{x}({\rm e}^{x}+1)^{2}}\)，当\(x<0\)时，\(g'(x)>0\)；当\(x>0\)时，\(g'(x)<0\)时，所以\(g(x)\)在\((-\infty,0)\)上单调递增，在\((0,+\infty)\)上单调递减，且\(g(x)\)在\(x=0\)处取得最大\(g(0)=1\)．
当\(a\geqslant 1\)时，\(y=a\)与\(g(x)\)至多有一个零点，不符合题意；
当\(a\leqslant 0\)时，由于当\(x\geqslant 0\)时，\(g(x)>0\)，而当\(x<0\)时，\(g(x)\)是单调递增，所以\(y=a\)与\(g(x)\)至多有一个交点，不符合题意；
当\(0<a<1\)时，一方面，由于\[g(-2)<0<a,g(0)=1>a,\]且\(g(x)\)在\((-2,0)\)上单调递增，所以\(y=a\)与\(g(x)\)在\((-2,0)\)上有且仅有一个交点．
另一方面，取\(x_{0}=\ln \dfrac{3}{a}\)，\[g(x_{0})=\dfrac{2{\rm e}^{x_{0}}+x_{0}}{{\rm e}^{2x_{0}}+{\rm e}^{x_{0}}}<\dfrac{3{\rm e}^{x_{0}}}{{\rm e}^{2x_{0}}}=\dfrac{3}{{\rm e}^{x_{0}}}=a,\]所以在\(\left(0,\ln \dfrac{3}{a}\right)\)上，有\[g(0)>a,\; g\left(\ln \dfrac{3}{a}\right)<a.\]且\(g(x)\)在区间\(\left(0,\ln \dfrac{3}{a}\right)\)上单调递减，于是\(y=a\)与\(g(x)\)在区间\(\left(0,\ln \dfrac{3}{a}\right)\)上有且仅有一个交点．
综上，当\(0<a<1\)时，函数\(f(x)\)有两个零点．