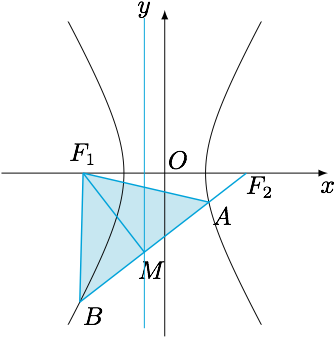
双曲线$x^2-\dfrac{y^2}{b^2}=1(b>0) $的左、右焦点分别为$F_1,F_2$,直线$l$过$F_2$且与双曲线交于$A,B$两点.
(1) 若$l$的倾斜角为$\dfrac{\pi}{2} $,$\triangle{F_1AB}$是等边三角形,求双曲线的渐近线方程;
(2) 设$b=\sqrt{3} $,若$l$的斜率存在,且$\left(\overrightarrow{F_1A}+\overrightarrow{F_1B} \right)\cdot\overrightarrow{AB}=0 $,求$l$的斜率.
解 (1)$y=\pm \sqrt{2}x $.
(2)如图,由题意,$A,B$两点分别位于双曲线的两支上,且$\left|AF_1\right|=\left|BF_1\right|$.设该双曲线的左准线为$l_1:x=-\dfrac{1}{2} $,线段$AB$的中点为$M$,则$A,B$两点分别位于左准线$l_1$的左右两边,且到$l_1$的距离相等,故点$M$落在$l_1$上.
设点$M$坐标为$\left(-\dfrac{1}{2},m\right) $,则$$\overrightarrow{F_1M}\cdot\overrightarrow{F_2M}=\left(\dfrac{3}{2},m \right)\cdot\left(-\dfrac{5}{2},m \right)=m^2-\dfrac{15}{4}= 0, $$解得$$m=\pm \dfrac{\sqrt{15} }{2}, $$所以直线$l$的斜率为$\pm \dfrac{\sqrt{15} }{5} $.