抛物线的一则常用性质

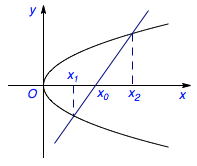
抛物线有一条非常简单优美的性质，设直线\(l\)与抛物线\(y^2=2px\)相交，则其横截距是两交点横坐标的等比中项．如图，有\(x_0^2=x_1x_2\)．

同学们可以拿这三道题目练练手：

• 2014年北京丰台区高三期末考试

  已知抛物线\(C:y^2=2px(p>0)\)的焦点为\(F(1,0)\)，点\(O\)为坐标原点，\(A\)，\(B\)是曲线\(C\)上异于\(O\)的两点．
  （1）求曲线\(C\)的方程；
  （2）若直线\(OA\)，\(OB\)的斜率之积为\(-\frac 12\)，求证：直线\(AB\)过定点．

  ---

• 2013年北京海淀区高三期末考试

  已知\(E(2,2)\)是抛物线\(C:y^2=2px\)上一点，经过点\(2,0\)的直线\(l\)与抛物线\(C\)交于\(A\)，\(B\)两点（不同于点\(E\)），直线\(EA\)，\(EB\)分别交直线\(x=-2\)于点\(M\)，\(N\)．
  （1）求抛物线方程及其焦点坐标；
  （2）已知\(O\)为原点，求证：\(\angle MON\)为定值．

  ---

• 2013年北京西城区高三期末考试

  已知抛物线\(y^2=4x\)的焦点为\(F\)，过点\(P(2,0)\)的直线交抛物线于\(A(x_1,y_1)\)，\(B(x_2,y_2)\)两点，直线\(AF\)，\(BF\)分别与抛物线交于点\(M\)，\(N\)．
  （1）求\(y_1y_2\)的值；
  （2）记直线\(MN\)的斜率为\(k_1\)，直线\(AB\)的斜率为\(k_2\)，证明：\(\dfrac {k_1}{k_2}\)为定值．