代数部分告一段落，最后两次留给平面几何．高中对平面几何的要求总体不高，但在解析几何与三角等问题中我们常常会涉及到一些平面几何的知识，这些知识属于爹不疼，娘不爱的类型：“高中老师说：你们初中应该学过！初中老师说：你们高中会学到的．”我们来关怀一下它们．遗忘系列包括：直角三角形的射影定理、角平分线定理、三角形四心相关的结论、四边形的边长与对角线长度的一些结论．
直角三角形的射影定理 在直角$\triangle ABC$中，直角顶点$C$在斜边$AB$上的射影为$D$（即$CD\perp AB$，且$D$为垂足），则有$$CD^2=AD\cdot BD,AC^2=AD\cdot AB,BC^2=BD\cdot AB.$$
可以通过证明$\triangle ABC$，$\triangle ACD$，$\triangle CBD$相似得到，具体过程略去．
例题一 在$\triangle ABC$中，$CD\perp AB$，$DE\perp AC$，$DF\perp BC$，垂足分别为$D,E,F$，求证：$\angle CAB=\angle CFE$．
证明 在$\mathrm{Rt}\triangle ACD$中，$DE\perp AC$，所以有$$CD^2=CE\cdot CA.$$在$\mathrm{Rt}\triangle BCD$中，$DF\perp BC$，所以有$$CD^2=CF\cdot CB.$$所以$$CE\cdot CA=CF\cdot CB\ \Rightarrow\ \dfrac{CE}{CB}=\dfrac {CF}{CA}.$$又因为$\angle ECF=\angle BCA$，所以$\triangle CEF\backsim \triangle CBA$，从而有$\angle CAB=\angle CFE$．
三角形的角平分线性质定理 在$\triangle ABC$中，$AD$是$\angle BAC$的角平分线，则有$\dfrac {BD}{CD}=\dfrac {AB}{AC}$．
证明 考虑$\triangle ABD$的面积$S_1$与$\triangle ACD$的面积$S_2$．如果以$AB,AC$为底边，由角平分线定理知，点$D$到$AB$的距离等于点$D$到$AC$的距离，如图：
所以有$S_1:S_2=AB:AC$；
再考虑以$BD,CD$为底边，此时两个三角形的高相同，有$S_1:S_2=BD:CD$；从而有$$\dfrac {S_1}{S_2}=\dfrac {AB}{AC}=\dfrac {BD}{CD},$$定理得证．
上面的定理事实上是三角形内角平分线的性质定理，是平面几何中很常用的一个定理，为了方便起见，我们把它简称为角平分线定理．此外，还有三角形外角平分线的性质定理：在$\triangle ABC$中，$AD$是$\angle BAC$的外角平分线，则有$\dfrac {BD}{CD}=\dfrac {AB}{AC}$．
可以用证明三角形内角平分线性质定理的方法去证明三角形外角平分线定理．注意，当$AB=AC$时，$D$不存在（也可以认为$D$点在无穷远处）；当$AB>AC$时，$D$在射线$BC$上；当$AB<AC$时，$D$在射线$CB$上．
在$\triangle ABC$中，$D$是$BC$上的一点，若$\dfrac {BD}{CD}=\dfrac {AB}{AC}$，则$AD$为$\angle BAC$的角平分线．称之为三角形角平分线的判定定理．
它的证明可以利用性质定理的思路，读者可以自行尝试．
例题二 已知$\triangle ABC$满足$AB=10,BC=12,AC=8$，射线$CI$平分$\angle ACB$，并交边$AB$于点$D$．
(1)求$AD,BD$的长；
(2)若点$E$在射线$CI$上，且满足$EA=EB$，求$\dfrac {CD}{DE}$的值；
(3)射线$CI$上是否存在一点$F$，使得$\dfrac {AC}{BC}=\dfrac {AF}{BF}$，若存在，求出$CF$的长；若不存在，说明理由．
分析与解 (1)由角平分线定理知$$\dfrac {AD}{BD}=\dfrac {AC}{BC}=\dfrac 23,$$所以$AD=4,BD=6$；
(2)如图，取$BC$的中点$N$，连结$EN$，则由$EA=EB$，知$EN\perp AB$，过点$C$作$CM\perp AB$于点$M$，如图：
则有$$\dfrac {CD}{DE}=\dfrac {DM}{DN},$$因为$DN=BD-BN=1$，下面去计算$DM$的值．设$DM=x$，分别在直角$\triangle ACM$与$\triangle BCM$中计算$CM$得到$$CM^2=8^2-(4-x)^2=12^2-(6+x)^2,$$计算得$x=3$．于是知$\dfrac {CD}{DE}=3$．
(3)若存在点$F$满足条件，则有$$\dfrac {AC}{BC}=\dfrac {AD}{BD}=\dfrac {AF}{BF},$$由三角形角平分线的判定定理知$FD$平分$\angle AFB$，从而有$\triangle ACF\cong\triangle BCF$，所以$AC=BC$，矛盾．所以点$F$不存在．
最后介绍两个四边形的边长与对角线的长度关系相关的结论，有时会在相关计算时用到，读者可以选择性学习：
结论一 对于平行四边形$ABCD$，有对角线的平方和等于四边的平方和，即$$AC^2+BD^2=2(AB^2+BC^2).$$结论二 对于凸四边形$ABCD$，有对角线的乘积不大于两组对边的乘积之和，即$$AC\cdot BD\leqslant AB\cdot CD+AD\cdot BC.$$当$ABCD$为圆的内接四边形时，等号成立，此时的结论被称为托勒密定理．
简要证明：
(1)过点$A,D$作$BC$边的垂线，交$BC$及其延长线于点$N,M$，如图：
于是有$$\begin{cases} AC^2=AN^2+(BC-BN)^2,\\BD^2=DM^2+(BC+CM)^2. \end{cases} $$又因为$AN=DM,BN=CM$，上面两式左右分别相加整理即得结论一．
(2)分别作$\angle BAE=\angle CAD,\angle ABE=\angle ACD$，交点为$E$，连结$DE$，如图：
则有$\triangle ABE\backsim\triangle ACD$，从而有$$\dfrac {BE}{CD}=\dfrac {AB}{AC}=\dfrac {AE}{AD},$$于是得到①式：$AB\cdot CD=AC\cdot BE$．又因为$$\angle BAC=\angle EAD,\dfrac {AB}{AC}=\dfrac {AE}{AD},$$所以有$\triangle BAC\backsim\triangle EAD$，从而有$$\dfrac {AB}{AE}=\dfrac {AC}{AD}=\dfrac {BC}{DE},$$于是得到②式：$AD\cdot BC=AC\cdot DE$．
将①②两式相加得$$AB\cdot CD+AD\cdot BC=AC\cdot(BE+DE)\geqslant AC\cdot BD,$$当且仅当$B,D,E$三点共线时取到等号，当$\angle ABD=\angle ACD$时这三点共线，此时$A,B,C,D$共圆．
例题三 正三角形$ABC$内接于圆$O$，点$P$是劣弧$BC$上任一点，$PA,BC$交于点$E$，有如下结论：①$PA=PB+PC$；②$\dfrac {1}{PA}=\dfrac 1{PB}+\dfrac {1}{PC}$；③$PA\cdot PE=PB\cdot PC$．其中正确的结论为_______．
分析与解 因为$ABPC$是圆的内接四边形，所以有$$PA\cdot BC=AB\cdot PC+AC\cdot BP,$$又因为$AB=BC=AC$，所以有$PA=PC+PB$，①正确；并由此知②错误；③通过$\triangle ABP\backsim\triangle CEP$知$$\dfrac {PA}{PC}=\dfrac {PB}{PE},$$从而有③正确．综上知，①③正确．
最后给出两道练习：
练习一 (1)已知直角$\triangle ABC$的直角边$AC=3,BC=4$，求斜边的中线$CM$，高$CH$与角平分线$CI$的长；
(2)已知三角形$ABC$的三边$AC=4,BC=5,AB=6$，求$AB$边上的中线$CM$，高$CH$，角平分线$CI$的长．
答案 (1)$CM=\dfrac 52,CH=\dfrac {12}{5},CI=\dfrac {12\sqrt 2}{7}$；
(2)$CM=\dfrac {\sqrt{46}}{2},CH=\dfrac {5\sqrt 7}{4},CI=\dfrac {10}{3}$．
提示 非直角三角形的中线长可以通过补全为平行四边形求解．
练习二 已知$A,B,C,D$四点共线，且满足$\dfrac {CA}{CB}=\dfrac {DA}{DB}=2$，若动点$P$满足$\dfrac {PA}{PB}=2$，证明点$P$在以$CD$为直径的圆上．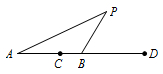
证明 由$\dfrac {PA}{PB}=\dfrac{AC}{BC}=\dfrac {AD}{DB}$知，$PC$平分$\angle APB$，且$PD$平分$\angle APB$的外角，如图：
所以$\angle BPC+\angle BPD=90^\circ$，所以$P$在以$CD$为直径的圆上．
小编的话 原计划在平面几何内容中还要介绍弦切角定理、切割线定理与相交弦定理，写起来才发现三角形与四边形中这些定理就已经非常丰富了，考虑到这些定理在高中的使用更靠前、遗弃更为彻底，所以圆中的定理我们放到高中的平面几何选讲中再作介绍．