朗博函数简介

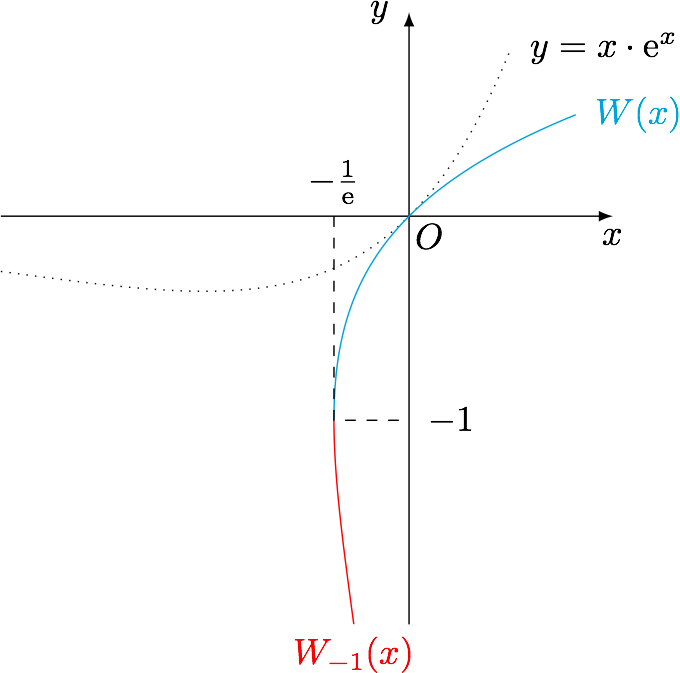
        朗博W函数(Lambert W Function)，又称欧米伽函数或乘积对数函数，是复变函数$f(x)=x\cdot \exp (x)$的反函数．如果我们把朗博函数的定义域限制在$\left[-\dfrac{1}{\rm e},+\infty\right)$上，取其在$[-1,+\infty)$上的函数值，那么就定义了一个单调递增的函数$W(x)$；同时将定义域在$\left(-\dfrac{1}{\rm e},0\right)$时，取其在$(-\infty,-1)$上的函数值，那么就定义了一个单调递减的函数$W_{-1}(x)$．

        在中学阶段通常用以解形如 $$x\cdot {\rm e}^x=a(a\geqslant 0)$$ 的方程(往往是超越方程)，将其实数根记为$W(a)$．当$a\in \left(-\dfrac{1}{\rm e},0\right)$时，方程有两个实根$W(a),W_{-1}(a)$．

        很多包含对数函数的超越方程也可以利用朗博函数求解，如 $$x\ln x=a,x+\ln x=a,\dfrac{\ln x}x=-a,$$ 其中$a\geqslant 0$．它们的解分别为 $$x={\rm e}^{W(a)},x=W({\rm e}^a),x={\rm e}^{-W(a)}.$$ 需要注意的是利用朗博函数的性质，可以作类似下面的化简： $${\rm e}^{-W(a)}=\dfrac{W(a)}{a}.$$

例一    若$\forall x>0,x{\rm e}^{2x}-kx-\ln x-1\geqslant 0$，求实数$k$的取值范围．

解    分离变量，记函数$f(x)={\rm e}^{2x}-\dfrac{\ln x}x-\dfrac 1x$，则问题的关键是求$f(x)$的最小值．函数$f(x)$的导函数 $$f'(x)=2{\rm e}^{2x}+\dfrac{\ln x}{x^2}=\dfrac 1x\left(2x{\rm e}^{2x}+\dfrac{\ln x}x\right).$$ 令 $$\begin{cases} 2x{\rm e}^{2x}=a,\\ \dfrac{\ln x}{x}=-a,\end{cases}$$ 则解得 $$x=\dfrac 12W(a)=\dfrac{W(a)}a,$$ 于是$a=2$，且极小值点为$x=\dfrac 12W(2)$，因此函数$f(x)$的极小值，亦为最小值是 $$f\left(\dfrac 12W(2)\right)=\dfrac{\dfrac 12W(2){\rm e}^{W(2)}-1}{\dfrac 12W(2)}+2=2,$$ 因此$k$的取值范围是$(-\infty ,2]$．

例二    若$\forall x\geqslant 0,{\rm e}^{mx}-mx^2-1\geqslant 0$，求正实数$m$的取值范围．

解    当$x=0$时，不等式显然成立．当$x>0$时，问题等价于 $$\forall x>0,{\rm e}^x-\dfrac{x^2}m-1\geqslant 0,$$ 即 $$\dfrac 1m\leqslant \dfrac{{\rm e}^x-1}{x^2},x>0.$$

令$f(x)=\dfrac{{\rm e}^x-1}{x^2}$，则其导函数 $$f'(x)=\dfrac{{\rm e}^x(x-2)+2}{x^3}.$$ 注意到方程 $${\rm e}^x(x-2)+2=0,$$ 即 $$(x-2){\rm e}^{x-2}=-2{\rm e}^{-2},$$ 因此函数$f(x)$的极小值点为$x=2+W(-2{\rm e}^{-2})$（注意舍去$x=2+W_{-1}(-2{\rm e}^{-2})$）．因此正实数$m$的取值范围是不等式 $$\dfrac 1m\leqslant f(2+W(-2{\rm e}^{-2}))$$ 的解，化简得$m$的取值范围是$\left[-W(-2{\rm e}^{-2})(W(-2{\rm e}^{-2})+2),+\infty\right)$．

注    $W(-2{\rm e}^{-2})\approx -0.4064$，从而$m$的取值范围约为$[0.6476,+\infty)$．

例三     若$\dfrac 12mx^2+(m-1)-1\geqslant \ln x$恒成立，求$m$的最小值．

解     分离变量可得 $$m\geqslant \dfrac{\ln x+x+1}{\dfrac 12x^2+x},$$ 设右侧函数为$\varphi(x)$，则其导函数 $$\varphi'(x)=\dfrac{\dfrac 12(x+1)(-x-2\ln x)}{\left(\dfrac 12x^2+x\right)^2},$$ 于是其极大值点为$x={\rm e}^{-W\left(\frac 12\right)}$，于是$m$的最小值为 $$\varphi\left({\rm e}^{-W\left(\frac 12\right)}\right)={\rm e}^{W\left(\frac 12\right)}.$$

注    ${\rm e}^{W\left(\frac 12\right)}\approx 0.7035$，${\rm e}^{-W\left(\frac 12\right)}\approx 1.4215$．

2017.5.23添加：

练习　若${\rm e}^x>a\ln x$对任意$x>1$恒成立，求实数$a$的取值范围．

解　考虑分离变量，问题即 $$\forall x>1,a<\dfrac{{\rm e}^x}{\ln x},$$ 记右侧函数为$\varphi(x)$，则其导函数 $$\varphi'(x)=\dfrac{{\rm e}^x\left(x\ln x-1\right)}{x\ln^2x},$$ 因此函数$\varphi(x)$在$x={\rm e}^{W(1)}$处取得极小值，亦为最小值．进而实数$a$的取值范围是$\left(-\infty,\dfrac{{\rm e}^{{\rm e}^{W(1)}}}{W(1)}\right)$．

注　其中$W(1)$(约等于$0.5671$)是方程$x{\rm e}^x=1$的解，$W(x)$称为朗博函数．