计数的映射方法简介

对于两个有限集合$M$、$N$，如果我们能够建立单射$f:M \to N$，那么${\rm{card}}(N)$（其中${\rm{card}}$表示有限集合中元素的数目）．进一步，如果我们能够证明$f$是满射，那么就可以得到${\rm{card}}(M )={\rm{card}}(N)$．这一简单结论在组合计数中应用很广泛，举例如下．

问题一    棋盘上的方格

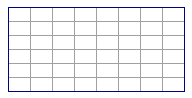
如图1，一个$m \times n$的棋盘（指包含边界在内有$m$条竖线和$n$条横线）．

（1）有多少个小正方形方格？

（2）有多少个“对顶”方格组（包括旋转对称后的形状）？

（1）解    设$M$是小正方形方格的集合，$N$是前$m-1$条竖线和$n-1$条横线形成的交点的集合．那么小正方形方格和$N$中的点是一一映射的，因此$${\rm{card}}(M) = {\rm{card}}(N)=(m-1)(n-1).$$

（2）解    设$M$是“对顶”方格组的集合，通过取两个小方格的公共点$P$以及形成方向$\tau$，于是$(P,\tau)$构成集合$N$．显然这也是一个一一映射，于是$${\rm{card}}(M) = {\rm{card}}(N)=2(m-2)(n-2).$$

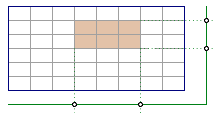
思考题    有多少个“犄角”方格组（包括旋转对称后的形状）呢？又有多少个“情侣”方格组（包括旋转后的形状）？（如图2）

答案分别为$4\left( {m-2} \right)\left( {n-2} \right)$和$(m-2)(n-1)+(m-1)(n-2)$．

提示    对于“犄角”，可以取中心点和缺角方向；对于“情侣”，可以取中间的小竖线或小横线．

 

问题二    棋盘上的“方格”

如图3，在一个$m \times n$的矩形网格（指包含边界在内有$m$条竖线和$n$条横线）中有多少个矩形？

解    如图4，横线上的两个不同点和竖线上的两个不同点与矩形一一对应，于是所求矩形数为$${\rm{C}}_m^2{\rm{C}}_n^2.$$

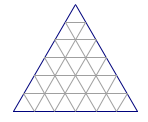
思考题    如图5，在一个$n$级正三角网格中有多少个平行四边形呢？

答案是$3{\rm{C}}_{n+2}^4$．

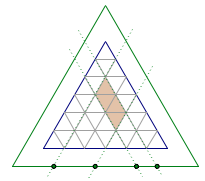
提示    如图6，每条横线上的四个不同点都与平行四边形一一对应．

问题三    圆周上的点

圆周上有$n$个点，用弦把它们连接起来，那么

（1）有多少条不同的弦？

（2）这些弦至多有多少个交点（指在圆内部的）？

（3）这些弦至多将圆分成多少个无公共部分的区域？

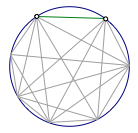
（1）解    如图7，圆上的两个无序点对与弦一一对应，因此数目为${\rm{C}}_n^2$；

（2）解    圆上的四个无序点对与交点一一对应（圆内接四边形对角线的交点），因此数目为${\rm{C}}_n^4$；

（3）解    新添一条弦$l$时，弦$l$与其他弦的交点将$l$分割为交点数加1条线段，每条线段都对应一个新增区域．因此所求数目为$1 + {\rm{C}}_n^2 + {\rm{C}}_n^4$．

思考题    平面上有$n$条直线，它们最多将平面分成多少个不同的无重叠部分的区域？

答案是${\rm C}_n^2+{\rm C}_n^1+1$．

问题四    数的拆分

将一个正整数$n$表示为${a_1} + {a_2} + \cdots + {a_p}$（$p \in {{\mathcal N}^ * }$）的形式，其中${a_i} \in {\mathcal{N}^ * }$，$i = 1,2, \cdots ,p$，且${a_1} \leqslant {a_2} \leqslant \cdots \leqslant {a_p}$，记所有这样的表示法的种数为$f\left( n \right)$（如$4 = 4$，$4 = 1 + 3$，$4 = 2 + 2$，$4 = 1 + 1 + 2$，$4 = 1 + 1 + 1 + 1$，故$f\left( 4 \right) = 5$）．对任意正整数$n$，比较$f\left( {n + 1} \right)$与$\dfrac{1}{2}\left[ {f\left( n \right) + f\left( {n + 2} \right)} \right]$的大小，并给出证明．

解    对任意正整数$n$，均有$$f\left( {n + 1} \right) \leqslant \dfrac{1}{2}\left[ {f\left( n \right) + f\left( {n + 2} \right)} \right],$$只需要证明$$f\left( {n + 2} \right) - f\left( {n + 1} \right) \geqslant f\left( {n + 1} \right) - f\left( n \right),$$证明如下：

注意到在$n$的所有表示法前加上“$1 + $”就可以得到$\left( {n + 1} \right)$的表示法中以$1$为第一项的表示法，因此$\left( {n + 1} \right)$的表示法中以$1$为第一项的有$f\left( n \right)$种，而不以$1$为第一项的有$f\left( {n + 1} \right) - f\left( n \right)$种；

类似的，$\left( {n + 2} \right)$的表示法中不以$1$为第一项的有$f\left( {n + 2} \right) - f\left( {n + 1} \right)$种；在$\left( {n + 1} \right)$的表示法中所有不以$1$为第一项的表示法中的最后一项加上$1$就可以得到$\left( {n + 2} \right)$的表示法中不以$1$为第一项的表示法，且这些表示法均不相同．这样就建立了从$\left( {n + 1} \right)$的不以$1$为第一项的表示法到$\left( {n + 2} \right)$的不以$1$为第一项的表示法的单射．

因此$$f\left( {n + 2} \right) - f\left( {n + 1} \right)\geqslant f\left( {n + 1} \right) - f\left( n \right).$$

注一    此题即2014年北京市海淀区第二次模拟考试理科数学压轴题．

注二    更多进阶内容，可以点击《卡特兰数 — 计数的映射方法的伟大胜利》．