已知正方体的棱长为\(1\)，求其最大截面面积．
下图是一个典型的错解，认为如图为最大截面，面积为\(6\times \dfrac {\sqrt 3}{4}\times \left(\dfrac {\sqrt 2}{2}\right)^2=\dfrac {3\sqrt 3}{4}.\)
正确的答案为\(\sqrt 2\)，如图所示．
我的解法如下，很繁琐，但不难．
解决立体几何问题的一般思路是将空间的几何问题转化为平面的几何问题，因此解决此问题的主要思路是利用面积射影定理，把空间的截面面积问题转化为底面上的投影的面积问题．
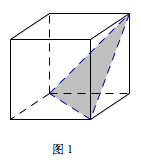
显然，当正方体的截面为三角形时，其最大面积的截面是边长为\(\sqrt 2\)的正三角形（如图1），面积为\(\dfrac {\sqrt 3}2<\sqrt 2\)．
而当正方体的截面不为三角形时，必然与正方体的一组相对的面均有交线\(l_1\)、\(l_2\)，将这组相对的面之一作为上下底面（如图2）．设截面在下底面上的投影面积为\(T\)，截面与下底面所成的二面角大小为\(\theta\)，则根据面积射影定理截面面积\[S=\dfrac T{\cos\theta}.\]
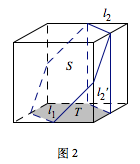根据面面平行的性质定理，交线\(l_2\)在底面上的投影\(l_2'\) 与交线\(l_1\)平行．设这两条平行线之间的距离为\(x\)，则容易求得\[\cos\theta=\dfrac x{\sqrt{x^2+1}},\]因此\[S=\sqrt{1+\dfrac 1{x^2}}\cdot T,0<x\leqslant\sqrt 2.\]
当\(x>1\)时，由于\(T\leqslant 1\)，因此\(S<\sqrt 2\)；
当\(0<x\leqslant 1\)时，我们研究当\(x\)固定时的投影面面积的最大值\(\max T(x)\)，再求出当\(x\)变化时的截面面积\(S\)的最大值\(\max S(x)\)即可．
记底面为正方形\(ABCD\)，下面按\(l_1\)和\(l_2'\)与正方形的四边的相交情况分类讨论（设相交得到的线段分别为\(MN\)和\(PQ\)）：
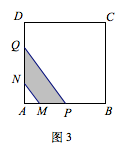
第一种情况，如图3，\(l_1\)与\(l_2'\)均与正方形的某一组邻边相交；
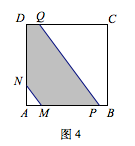
第二种情况，如图4，\(l_1\)与\(l_2'\)中一条与正方形的某一组邻边相交，另一条与某一组对边相交．
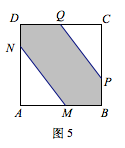
第三种情况，如图5，\(l_1\)与\(l_2'\)分别于正方形的两组邻边相交；
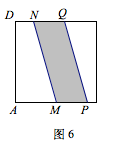
第四种情况，如图6，\(l_1\)与\(l_2'\)均与正方形的某一组对边相交．
利用微元法的思想，容易知道投影面积的最大值不可能在第一、二种情况取得．因为当我们将\(l_1\)、\(l_2'\)向右上方作平行移动时面积总会变大，最终将转化为第三、四种情况．
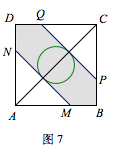
第三种情况中，继续利用微元法的思想可知当\(MN\)的方向固定时，\(MN\)的长度与\(PQ\)的长度相等时，投影面积达到最大．于是问题转化为以正方形中心为圆心，\(\dfrac x2\)为半径作圆，直线\(MN\)与圆相切且分别交\(AB\)、\(AD\)于\(M\)、\(N\)，求\(\triangle AMN\)的面积何时最小（如图7）．
容易证明，当\(MN\)与对角线\(AC\)垂直时取得最值，进而可以求得此时投影面积为\[\sqrt 2x-\dfrac 12x^2.\]
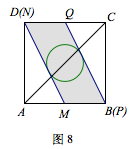
第四种情况比较简单，与第三种情况类似的作圆，显然当\(MN\)和\(PQ\)都过正方形顶点时投影面积最大，此时可以求得投影面积为\[\dfrac {2x}{\sqrt {2-x^2}+x}.\]
综上，我们得到了\[\max T(x)=\max\left(\sqrt2x-\dfrac 12x^2,\dfrac {2x}{\sqrt{2-x^2}+x}\right),\]于是
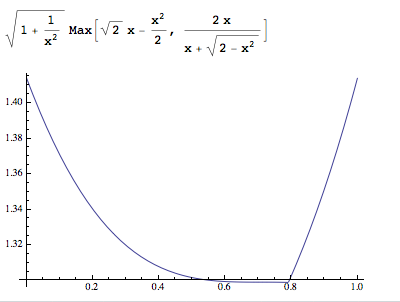
\[S_{\max}=\max\limits_{0<x\leqslant 1}\left(\sqrt {1+\dfrac 1{x^2}}\cdot \max\left(\sqrt2x-\dfrac 12x^2,\dfrac {2x}{\sqrt{2-x^2}+x}\right)\right).\]
由于此函数比较复杂，我们选择用mathematics画出对应函数图象如下：
观察函数图象可得当\(x=1\)时\(S_{\max}\)最大，为\(\sqrt 2\)，此时\(\cos\theta=\dfrac {\sqrt 2}2\)，\(\theta=\dfrac {\pi}4\)．所以棱长为\(1\)的正方体的最大截面面积为\(\sqrt 2\)，在\(x=1\)，\(\theta=\dfrac {\pi}4\)（此时截面即对角面）取得（另外当\(x\)趋近于\(0\)时，截面面积的最大值也趋于\(\sqrt 2\)，这恰好是垂直于底面的对角面，与实际情形吻合．）
从这个问题的解决过程可以看到：
1、貌似简单的问题，背后往往蕴含着深刻的数学思想方法；
2、好的问题引发有效的思考，对提高我们的思维品质和数学建模能力都非常有帮助．
由此可见，我们平时吃的麻辣烫里的鱼豆腐都切成这个样子，确实对尽快煮熟以及入味有帮助啊．